题目内容
已知函数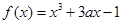 ,
, ,其中
,其中 是
是 的导函数.
的导函数.(1)对满足
 的一切
的一切 的值,都有
的值,都有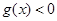 ,求实数
,求实数 的取值范围;
的取值范围;(2)设
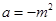 ,当实数
,当实数 在什么范围内变化时,函数
在什么范围内变化时,函数 的图象与直线
的图象与直线 只有一个公共点.
只有一个公共点.
(1)由题意,得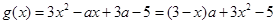 ,
,
设 ,
,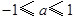 .
.
对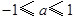 中任意
中任意 值,恒有
值,恒有 ,即
,即 ,
,
 即
即
解得 .
.
故 时,对满足
时,对满足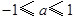 的一切
的一切 的值,都有
的值,都有 ;
;
(2) ,
,
①当 时,
时, 的图象与直线
的图象与直线 只有一个公共点;
只有一个公共点;
②当 时,列表:
时,列表:
 ,
,
又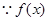 的值域是
的值域是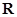 ,且在
,且在 上单调递增,
上单调递增,
 当
当 时,函数
时,函数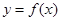 的图象与直线
的图象与直线 只有一个公共点.
只有一个公共点.
当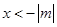 时,恒有
时,恒有 ,
,
由题意,得 ,
,
即 ,
,
解得 .
.
综上,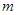 的取值范围是
的取值范围是 解析:
解析:
(1)先求出 ,当
,当 时,
时, 恒成立,所以令
恒成立,所以令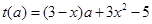 ,则只需
,则只需 ,解此关于x的不等式即可.
,解此关于x的不等式即可.
(2) 本小题要利用导数研究出y=f(x)的极值及图像,然后利用直线y=3与函数y=f(x)只有一个公共点时得到关于m的不等式,即可解出m的取值范围.
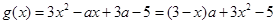 ,
,设
 ,
,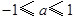 .
.对
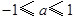 中任意
中任意 值,恒有
值,恒有 ,即
,即 ,
, 即
即
解得
 .
.故
 时,对满足
时,对满足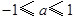 的一切
的一切 的值,都有
的值,都有 ;
;(2)
 ,
,①当
 时,
时, 的图象与直线
的图象与直线 只有一个公共点;
只有一个公共点;②当
 时,列表:
时,列表: |  |  |  |  |  |
 | 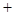 |  | 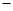 |  | 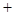 |
 |  | 极大值 |  | 最小值 |  |
 ,
,又
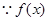 的值域是
的值域是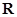 ,且在
,且在 上单调递增,
上单调递增, 当
当 时,函数
时,函数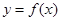 的图象与直线
的图象与直线 只有一个公共点.
只有一个公共点.当
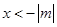 时,恒有
时,恒有 ,
,由题意,得
 ,
,即
 ,
,解得
 .
.综上,
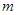 的取值范围是
的取值范围是 解析:
解析:(1)先求出
 ,当
,当 时,
时, 恒成立,所以令
恒成立,所以令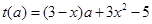 ,则只需
,则只需 ,解此关于x的不等式即可.
,解此关于x的不等式即可.(2) 本小题要利用导数研究出y=f(x)的极值及图像,然后利用直线y=3与函数y=f(x)只有一个公共点时得到关于m的不等式,即可解出m的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目