Question

【题目】已知，在平面直角坐标系中，直线AB与Y轴正半轴、X轴正半轴分别交于A、B两点，点A坐标为A（0，m），点B坐标为B（n，0），且满足（m﹣3）1+ =0，

（1）分别求出点A，点B的坐标
（2）若点E在直线AB上，且满足三角形AOE的面积等于三角形AOB的面积的三分之一，求点E的坐标．
（3）平移线段BAZ至DC，B与O是对应点，A与C是对应点，连接AC，E为BA腐乳延长线上一点，连接OE，OF平分∠COE，AF平分∠EAC，OF交AF于F点，若∠ABO+∠OEB=α．请在图2中将图形补充完整，并求∠F（用含α的式子表示）

Answer 1

【答案】
（1）

解：由非负数的性质得，m﹣3=0，n﹣4=0，

解得m=3，n=4，

所以，A（0，3）B（4，0）

（2）

解：设点E的横坐标为a，

∵S△AOE= S△AOB，

∴ ×3（﹣a）= × ×3×4，

解得a=﹣ ，

设直线AB的解析式为y=kx+b，

则 ，

解得 ，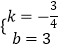

所以，直线AB的解析式为y=﹣ x+3，

当x=﹣ 时，y=﹣ ×（﹣ ）+3=1+3=4，

所以，点E的坐标为（﹣ ，4）

（3）

解：由平移的性质，AB∥OC，AC∥OB，

∴∠OEB=∠COE，∠CAE=∠ABO，

∵OF平分∠COE，AF平分∠EAC，

∴∠EAF= ∠CAE，∠EOF= ∠COE，

由三角形的内角和定理，∠OEB+∠EAF=∠F+∠EOF，

∠OEB+ ∠CAE=∠F+ ∠COE，

∴∠F=∠OEB+ ∠CAE﹣ ∠COE=∠OEB+ ∠CAE﹣ ∠OEB= （∠CAE+∠OEB），

∵∠ABO+∠OEB=α，

∴∠F= ．

【解析】（1）根据非负数的性质列式求出m、n的值，然后写出点A、B的坐标即可；（2）设点E的横坐标为a，然后利用三角形的面积列式求出a的值，再利用待定系数法求出直线AB的解析式，然后求解即可；（3）根据平移的性质可得AB∥OC，AC∥OB，根据平行线的性质可得∠OEB=∠COE，∠CAE=∠ABO，然后根据角平分线的定义可得∠EAF= ∠CAE，∠EOF= ∠COE，再根据三角形的内角和定理列式整理即可得解．
【考点精析】本题主要考查了坐标确定位置的相关知识点，需要掌握对于平面内任一点P，过P分别向x轴，y轴作垂线，垂足分别在x轴，y轴上，对应的数a,b分别叫点P的横坐标和纵坐标才能正确解答此题．