题目内容
19.已知函数f(x)定义域为[0,+∞),当x∈[0,1]时,f(x)=sinπx,当x∈[n,n+1]时,f(x)=$\frac{f(x-n)}{{2}^{n}}$,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是( )| A. | (0,1) | B. | ($\frac{1}{{2}^{1007}}$,$\frac{1}{{2}^{1006}}$) | C. | ($\frac{1}{{2}^{2017}}$,$\frac{1}{{2}^{2016}}$) | D. | ($\frac{1}{{2}^{1008}}$,$\frac{1}{{2}^{1007}}$) |
分析 根据题意,画出函数f(x)的图象,结合图象总结出函数f(x)的图象与直线y=b的交点情况,从而得出b的取值范围.
解答 解:根据题意,x∈[0,1]时,f(x)=sinπx,
x∈[n,n+1]时,f(x)=$\frac{f(x-n)}{{2}^{n}}$,其中n∈N,
∴f(n)=sinnπ=0,
f($\frac{1}{2}$)=sin$\frac{π}{2}$=1,
f($\frac{3}{2}$)=$\frac{f(\frac{3}{2}-1)}{2}$=$\frac{f(\frac{1}{2})}{2}$=$\frac{1}{2}$,
f($\frac{5}{2}$)=$\frac{f(\frac{5}{2}-2)}{{2}^{2}}$=$\frac{f(\frac{1}{2})}{4}$=$\frac{1}{4}$,…;
画出图形如图所示;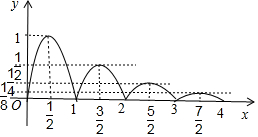
当b∈($\frac{1}{2}$,1)时,函数f(x)的图象与直线y=b有2个交点;
当b∈($\frac{1}{4}$,$\frac{1}{2}$)时,函数f(x)的图象与直线y=b有4个交点;
当b∈($\frac{1}{8}$,$\frac{1}{4}$)时,函数f(x)的图象与直线y=b有6个交点;…;
当b∈($\frac{1}{{2}^{1008}}$,$\frac{1}{{2}^{1007}}$)时,函数f(x)的图象与直线y=b有2016个交点.
故选:D.
点评 本题考查了函数的定义与性质以及函数图象的应用问题,是较难的题目.

练习册系列答案
相关题目
7.已知曲线y=f(x)在x=5处的切线方程是y=-x+5,则f(5)与f'(5)分别为( )
| A. | 3,3 | B. | 3,-1 | C. | -1,3 | D. | 0,-1 |
4.如果x=[x]+{x},[x]∈Z,0≤{x}<1,就称[x]表示x的整数部分,{x}表示x的小数部分.已知数列{an}满足a1=$\sqrt{5}$,an+1=[an]+$\frac{2}{\{{a}_{n}\}}$,则a2017-a2016等于( )
| A. | 2017+$\sqrt{5}$ | B. | 2016-$\sqrt{5}$ | C. | 6-$\sqrt{5}$ | D. | 6+$\sqrt{5}$ |
1.已知实数a<0,函数$f(x)=\left\{\begin{array}{l}{x^2}+2a,\;x<1\\-x,x≥1\end{array}\right.$,若f(1-a)≥f(1+a),则实数a的取值范围是( )
| A. | (-∞,-2] | B. | [-2,-1] | C. | [-1,0) | D. | (-∞,0) |
2.下列不等式正确的是( )
| A. | a3>a2(a>0,且a≠1) | B. | 0.30.8>0.30.7 | C. | π-1>e-1 | D. | log34>log43 |