题目内容
(本小题满分13分)已知函数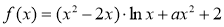 .
.
(1)当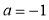 时,求
时,求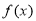 在
在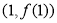 处的切线方程;
处的切线方程;
(2)设函数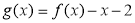 ,
,
(ⅰ)若函数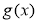 有且仅有一个零点时,求
有且仅有一个零点时,求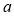 的值;
的值;
(ⅱ)在(ⅰ)的条件下,若 ,
,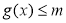 ,求
,求 的取值范围.
的取值范围.
(1) ;(2) (ⅰ)
;(2) (ⅰ) ;(ⅱ)
;(ⅱ) .
.
【解析】
试题分析: (1)对函数 求导,求出
求导,求出 ,即可求出切线方程;
,即可求出切线方程;
(2)(ⅰ)分离参数得 ,由函数
,由函数 的单调性可知,
的单调性可知, ,可求得
,可求得 ;(ⅱ)研究函数
;(ⅱ)研究函数 的单调性,求出函数
的单调性,求出函数 在区间
在区间 上的最大值即可.
上的最大值即可.
试题解析:(1)当 时,
时, 定义域
定义域 ,
,

 ,又
,又
 在
在 处的切线方程
处的切线方程 4分
4分
(2)(ⅰ)令
则
即
令 ,
,
则
令
 ,
,
 ,
, 在
在 上是减函数
上是减函数
又
所以当 时,
时, ,当
,当 时,
时, ,
,
所以 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,

所以当函数 有且今有一个零点时,
有且今有一个零点时, 9分
9分
(ⅱ)当 ,
, ,若
,若 只需证明
只需证明

令 得
得 或
或
又 ,
,
 函数
函数 在
在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增
上单调递增
又 ,
, 


即

 13分
13分
考点:导数的几何意义,导数与函数的单调性、极值、最值、函数零点.

(本小题满分12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(Ⅱ)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下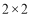 列联表:
列联表:
接受挑战 | 不接受挑战 | 合计 | |
男性 | 45 | 15 | 60 |
女性 | 25 | 15 | 40 |
合计 | 70 | 30 | 100 |
根据表中数据,能否在犯错误的概率不超过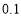 的前提下认为“冰桶挑战赛与受邀者的性别有关”?
的前提下认为“冰桶挑战赛与受邀者的性别有关”?
附: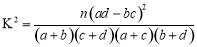
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
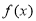 的定义域为开区间
的定义域为开区间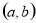 ,导函数
,导函数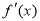 在
在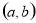 内的图象如图所示,则函数
内的图象如图所示,则函数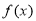 在开区间
在开区间 内的极小值点的个数为 个.
内的极小值点的个数为 个. 
 ,化简:
,化简:
 ,
, ,试用
,试用 表示
表示
 为定义在R上的奇函数,且在
为定义在R上的奇函数,且在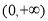 内是增函数,又
内是增函数,又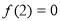 ,则不等式
,则不等式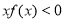 的解集为( )
的解集为( )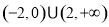

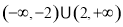
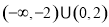
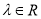 ,
,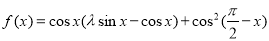 满足
满足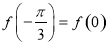 .
. 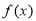 的单调递增区间;
的单调递增区间;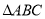 三内角
三内角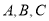 所对边分别为
所对边分别为 且
且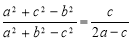 ,求
,求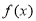 在
在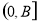 上的值域.
上的值域.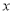 的方程
的方程 在区间[k-1,k+1]上有两个不相等的实根,则实数
在区间[k-1,k+1]上有两个不相等的实根,则实数 的取值范围是( )
的取值范围是( )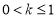 B.
B. C.
C.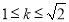 D.
D.
 为圆心,并且与直线
为圆心,并且与直线 相切的圆的方程为 .
相切的圆的方程为 .
