题目内容
6.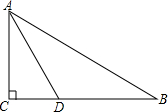 如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,若AD=4,求△ABC的周长.
如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,若AD=4,求△ABC的周长.
分析 首先根据角平分线的性质可得∠CAD=∠DAB=$\frac{1}{2}$∠CAB=30°,再根据等角对等边可得BD=AD,再根据在直角三角形中,30°角所对的直角边等于斜边的一半可得CD长,进而可得答案.
解答 解:∵∠C=90°∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的角平分线,
∴∠CAD=∠DAB=$\frac{1}{2}$∠CAB=30°,
∴BD=AD=4,CD=$\frac{1}{2}$AD,
∴CD=2,
∴BC=6,AC=$\sqrt{A{D}^{2}-C{D}^{2}}$=2$\sqrt{3}$,
∴AB=2AC=4$\sqrt{3}$,
∴△ABC的周长=6+2$\sqrt{3}$+4$\sqrt{3}$=6+6$\sqrt{3}$.
点评 此题主要考查了直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.如果关于x的二次函数y=x2-2mx+p的图象与端点为(-1,2)和(3,5)的线段只有一个交点,则p的值可能是( )
| A. | $\frac{5}{2}$ | B. | -$\frac{3}{2}$ | C. | 2 | D. | -1 |
15.若y<0<x,则$\frac{y+1}{x+1}$-$\frac{y}{x}$的结果为( )
| A. | 0 | B. | 正数 | C. | 负数 | D. | 整数 |