题目内容
9. 将长方形纸片按如图所示方式折叠,BC、BD为折痕,若∠ABC=35°,求∠ABD的度数.
将长方形纸片按如图所示方式折叠,BC、BD为折痕,若∠ABC=35°,求∠ABD的度数.
分析 根据折叠的性质得∠ABC=∠1,∠ABD=∠2,然后根据平角的定义计算.
解答 解:由题意知∠ABC=∠1,∠ABD=∠2,如图:
∴∠ABD=$\frac{1}{2}(180°-35°-35°)=55°$
点评 本题考查了角的计算:1°=60′,1′=60″.关键是根据折叠的性质得∠ABC=∠1,∠ABD=∠2.

练习册系列答案
相关题目
19.在一次气象探测活动中,1号探测气球从海拔5米处开始,以1米/分的速度竖直上升;与此同时,2号探测气球从海拔15米处开始,以0.5米/分的速度竖直上升.设两球同时上升的时间为x分(x小于50).下列结论中错误的是( )
| A. | 两球上升中的海拔高度分别为1号(x+5)米,2号(0.5x+15)米 | |
| B. | 上升10分钟时1号气球的海拔高于2号气球 | |
| C. | 上升20分钟时两只气球的海拔高度相等 | |
| D. | 当x大于20时,1号气球的海拔高度比2号气球的高(0.5x-10)米 |
20.一件商品的原价是118元,经过两次提价后的价格为168元.如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
| A. | 118(1+x)=168 | B. | 118(1+2x)=168 | C. | 118(1-x)2=168 | D. | 118(1+x)2=168 |
17.已知线段AB=5cm,BC=3cm,则线段AC的长度是( )
| A. | 8cm | B. | 2cm | C. | 8cm或2cm | D. | 无法确定 |
1. 如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )
如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )
 如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )
如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )| A. | (0,2) | B. | (0,$\frac{5}{3}$) | C. | (0,$\frac{4}{3}$) | D. | (0,$\frac{3}{2}$) |
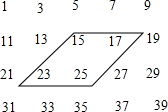 如图所示的数据是小明同学用一些奇数排成的,你能与小明一起探讨下列问题吗?动手试一试
如图所示的数据是小明同学用一些奇数排成的,你能与小明一起探讨下列问题吗?动手试一试