题目内容
6.解不等式(组),并把解集表示在数轴上(1)2(x+5)<3(x-5)
(2)$\left\{\begin{array}{l}{3(x+2)<x+8}\\{\frac{x}{2}≤\frac{x-1}{3}}\end{array}\right.$.
分析 (1)先去括号,再移项,合并同类项,把x的系数化为1,并在数轴上表示出来即可;
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)去括号得,2x+10<3x-15,
移项得,2x-3x<-15-10,
合并同类项得,-x<-25,
把x的系数化为1得,x>25,
在数轴上表示为: ;
;
(2)$\left\{\begin{array}{l}3(x+2)<x+8①\\ \frac{x}{2}≤\frac{x-1}{3}②\end{array}\right.$,由①得,x<1,由②得,x≤-2,
故不等式组的解集为:x≤-2.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知同大取大;同小取小;大小小大中间找;大大小小找不到的原则是解答此题的关键.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
17.在+1,-2,-1这三个数中,任取两个数相加,所得的和最大的是( )
| A. | -1 | B. | 1 | C. | 0 | D. | -3 |
18.下列方程中是一元二次方程的是( )
| A. | x2+1=0 | B. | y2+x=1 | C. | 2x+1=0 | D. | x+$\frac{1}{x}$=1 |
15.若132x=64,则13-x=( )
| A. | -$\frac{1}{8}$ | B. | ±$\frac{1}{8}$ | C. | $\frac{1}{80}$ | D. | $\frac{1}{512}$ |
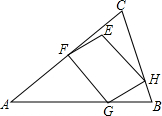 如图,在△ABC中,AB=AC=1,∠A=36°,?EFGH的顶点F,G,H分别在AC,AB,BC边上,且FC=CH.
如图,在△ABC中,AB=AC=1,∠A=36°,?EFGH的顶点F,G,H分别在AC,AB,BC边上,且FC=CH.