题目内容
12.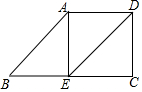 如图,已知在四边形中ABCD,AD∥BC,过点A作AE⊥BC于点E,连接DE,∠BAE=46°,且△ABE≌△EDA.
如图,已知在四边形中ABCD,AD∥BC,过点A作AE⊥BC于点E,连接DE,∠BAE=46°,且△ABE≌△EDA.(1)求∠ADE的度数;
(2)若△EDA≌△DEC,试判断AE与CD之间的数量关系和位置关系,并说明理由.
分析 (1)根据平行线的性质得到AE⊥AD,根据三角形的内角和得到∠B=44°,根据全等三角形的性质即可得到结论;
(2)根据全等三角形的性质即可得到结论.
解答 解:(1)∵AD∥BC,AE⊥BC,
∴AE⊥AD,
∴∠EAD=90°,
∵∠BAE=46°,
∴∠B=44°,
∵△ABE≌△EDA,
∴∠ADE的度数为44°;
(2)AE=CD,且AE∥CD;
理由∵△EDA≌△DEC,
∴AE=CD,∠AED=∠CDE,
∴AE∥CD.
点评 本题考查了全等三角形的性质,平行线的判定,熟练掌握全等三角形的性质是解题的关键.

练习册系列答案
相关题目
3.$\sqrt{3-m}$的相反数为( )
| A. | -$\sqrt{3-m}$ | B. | $\sqrt{m-3}$ | C. | $\sqrt{3-m}$ | D. | $\frac{\sqrt{3-m}}{3-m}$ |
7.下列各式变形错误的是( )
| A. | 3m+4=0变形为3m=-4 | B. | $\frac{x+4}{3}$=1-x变形为x+4=3-3x | ||
| C. | -5(x-2)=-5变形为x-2=1 | D. | -$\frac{x+1}{3}$=$\frac{1}{3}$变形为-x+1=1 |
17.已知一次函数y=kx+7和y=k′x+5,假设k>0且k′<0,则这两个一次函数的图象的交点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.点M(3,-4)关于y的轴的对称点是M1,则M1关于x轴的对称点M2的坐标为( )
| A. | (-3,4) | B. | (-3,-4) | C. | (3,4) | D. | (3,-4) |
1.大于-2.5而小于$\root{3}{46}$的整数共有( )
| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
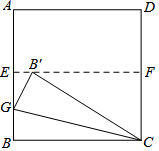 如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.则∠B′GC=75度.
如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.则∠B′GC=75度.