题目内容
18.如图1,在线段BE上取一点C,分别以CB,CE为腰作等腰直角△BCA和等腰直角△DCE,连接BD和AE.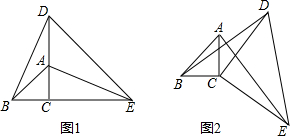
(1)请判断线段BD和线段AE的数量关系,并说明理由;
(2)如图2,若B,C,E 三点不共线,(1)中的结论还成立吗?请说明理由.
分析 (1)依据等腰直角三角形的性质可得到BC=AC,DC=CE,∠BCD=∠ACE=90°,然后依据SAS证明△BCD≌△ACE,接下来,依据全等三角形的性质可得到BD=AE;
(2)依据等腰直角三角形的性质可得到BC=AC,DC=CE,∠BCD=∠ACE=90°,然后利用等式的性质证明∠BCD=∠ACE,然后依据SAS证明△BCD≌△ACE,接下来,依据全等三角形的性质可得到BD=AE.
解答 解:(1)∵△BCA和△DCE均为等腰直角三角形,
∴BC=AC,DC=CE,∠BCD=∠ACE=90°.
在△BCD和△ACE中$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=CE}\end{array}\right.$,
∴△BCD≌△ACE.
∴BD=AE.
(2)成立.
∵△BCA和△DCE均为等腰直角三角形,
∴BC=AC,DC=CE,∠BCD=∠ACE=90°.
∴∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE.
在△BCD和△ACE中$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=CE}\end{array}\right.$,
∴△BCD≌△ACE.
∴BD=AE.
点评 本题主要考查的是全等三角形的性质和判定、等腰直角三角形的性质,熟练掌握相关知识是解题的关键.

练习册系列答案
相关题目
6.下列方程中,属于一元二次方程的是( )
| A. | x2-$\frac{1}{x}$=1 | B. | x2+y=2 | C. | $\sqrt{2}$x2=2 | D. | x+5=-7 |
10.下列选项不是同类项的是( )
| A. | -3和6 | B. | -4x2yz和2yzx2 | C. | 2ab2和2a2b | D. | 9a3和-a3 |

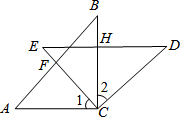 如图,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.
如图,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.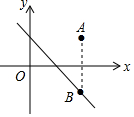 如图,在平面直角坐标系中点A(2,m)在第-象限,若点A关于x轴的对称点B在直线y=-x+1上,求m的值.
如图,在平面直角坐标系中点A(2,m)在第-象限,若点A关于x轴的对称点B在直线y=-x+1上,求m的值. 如图实数在数轴上表示为:化简:$\sqrt{{a}^{2}}$-|a-b|-|c-a|+$\sqrt{(b-c)^{2}}$.
如图实数在数轴上表示为:化简:$\sqrt{{a}^{2}}$-|a-b|-|c-a|+$\sqrt{(b-c)^{2}}$.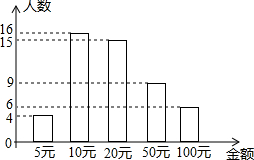 如图所示是某班50名学生的捐款情况统计图,根据图中信息可得捐款金额的中位数是20元.
如图所示是某班50名学生的捐款情况统计图,根据图中信息可得捐款金额的中位数是20元.