题目内容
9.已知:x2-4x+1=0,求下列各式的值:(1)x2+x-2;
(2)x4+x-4.
分析 (1)先根据题意得出x2=4x-1,再根据负整数指数幂的运算法则把原式进行化简,再把x2的值代入进行计算即可;
(2)根据负整数指数幂的运算法则把原式进行化简,再把(1)中的结果代入进行计算即可.
解答 解:(1)∵x2-4x+1=0,
∴x2=4x-1,
∴x2+x-2
=x2+$\frac{1}{{x}^{2}}$
=$\frac{{x}^{4}+1}{{x}^{2}}$
=$\frac{(4x-1)^{2}+1}{4x-1}$
=$\frac{16{x}^{2}-8x+1+1}{4x-1}$
=$\frac{16(4x-1)-8x+2}{4x-1}$=$\frac{64x-16-8x+2}{4x-1}$
=$\frac{56x-14}{4x-1}$
=$\frac{14(4x-1)}{4x-1}$
=14;
(2)x4+x-4
=x4+$\frac{1}{{x}^{4}}$
=(x2+$\frac{1}{{x}^{2}}$)2-2
=142-2
=194.
点评 本题考查的是负整数指数幂,熟知负整数指数幂等于对应的正整数指数幂的倒数是解答此题的关键.

练习册系列答案
相关题目
14.如果方程2x2n-7-1=4是关于x的一元一次方程,则n的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 在⊙O中,AB、BC、CD为弦,∠E=60°,∠F=80°,求∠A.
在⊙O中,AB、BC、CD为弦,∠E=60°,∠F=80°,求∠A.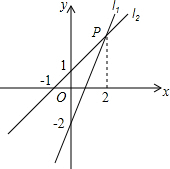 如图,过点(0,-2)的直线l1:y=kx+b(k≠0)与直线l2:y=x+1交于点P(2,m).
如图,过点(0,-2)的直线l1:y=kx+b(k≠0)与直线l2:y=x+1交于点P(2,m). 如图,在⊙O中,半径OC⊥AB,AC=2$\sqrt{3}$,CD=2,求⊙O的半径OA的长.
如图,在⊙O中,半径OC⊥AB,AC=2$\sqrt{3}$,CD=2,求⊙O的半径OA的长.