题目内容
3.(1)求上午10时30分,钟面上时针和分针的夹角.(2)在上午10时30分到11时30分之间,时针和分针何时成直角?
(3)在0时到12时之间,钟面上的时针与分针在什么时候成60°的角?试尽可能多地找出答案,又秒针与时针共有几次成60°的角?
分析 (1)根据时针与分针相距的份数乘以每份的度数,可得答案;
(2)利用时针和分针所成角度的和与差是90°列出方程解答即可;
(3)分针的速度为每分钟1个单位长度,则时针的速度为每分钟$\frac{1}{12}$个单位长度,将时针、分针看成两个不同速度的人在环形跑道上同时(从0时开始)开始同向而行,要求两者相距10个或50单位长度所用的时间,由此列出方程解答即可.
解答 解:(1)钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,
上午10时30分,钟面上时针和分针的夹角是4.5个等份,因而时针和分针的夹角是4.5×30=135°;
(2)时针一小时即60分钟转30度,一分钟转动0.5°,分针一小时转360度,一分钟转6度,
可以设从上午10时30分再经过x分钟,时针和分针成直角,
列方程得到:135-6x+0.5x=90,
解得x=8$\frac{2}{11}$,即10时38$\frac{2}{11}$分时,时针和分针成直角;
11时时针与分针的夹角是30度,设再过y分钟,时针与分针的夹角是直角,
根据题意得到:30+6y-0.5y=90,解得y=10$\frac{10}{11}$,
则当在11时10$\frac{10}{11}$分时,时针和分针成直角.
(3)设从0时开始,过x分钟后分针与时针成60°的角,此时分针比时针多走了n圈(n=0,1,2,…,11),
则x-$\frac{x}{12}$=60n+10或x-$\frac{x}{12}$=60n+50,
解得x=$\frac{12}{11}$(60n+10)或x=$\frac{12}{11}$(60n+10).
分别令n=0,1,2,3,…,11,即得本题的所有解(精确到秒),共22个:
0:10:55 1:16:22 2:21:49 3:27:16 4:32:44 5:38:11
6:43:38 7:49:05 8:54:33 10:00:00 11:05:27
0:54:33 2:00:00 3:05:27 4:10:55 5:16:22 6:21:49
7:27:16 8:32:44 9:38:11 10:43:38 11:49:05
在12个小时内,秒针相对于时针走了60×12-1=719圈,所以秒针与时针共有719×2=1438次成60°的角.
点评 此题考查一元一次方程的实际运用,搞清利用起点时间时针和分针的位置关系是解决问题的关键.

 如图,方格纸中的每个小正方形的边长为1.则图中的格点四边形ABCD的面积为( )
如图,方格纸中的每个小正方形的边长为1.则图中的格点四边形ABCD的面积为( )| A. | 6.5 | B. | 7 | C. | 7.5 | D. | 8 |
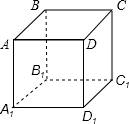 如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着正方体表面什么路径爬行,才能最快吃到蜜糖.请画出正方体的展开图及蚂蚁爬行的路线.
如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着正方体表面什么路径爬行,才能最快吃到蜜糖.请画出正方体的展开图及蚂蚁爬行的路线.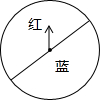 如图是一个红,蓝两色各占一半的转盘,小李与小明做“配紫色”的游戏.规则是:两人各让转盘自由转动一次.当转盘停止转动时.如果指针所在区域的颜色配成紫色.小明胜:如果指针所在区域的颜色配不成紫色.小李胜.在这个游戏中.小李与小明获胜的概率分别是多少?该游戏规则对双方公平吗?为什么?
如图是一个红,蓝两色各占一半的转盘,小李与小明做“配紫色”的游戏.规则是:两人各让转盘自由转动一次.当转盘停止转动时.如果指针所在区域的颜色配成紫色.小明胜:如果指针所在区域的颜色配不成紫色.小李胜.在这个游戏中.小李与小明获胜的概率分别是多少?该游戏规则对双方公平吗?为什么?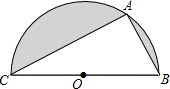 半圆内有一个直角三角形ABC,AB长为a厘米,AC长为b厘米,半圆的半径为r厘米,解答下面各题:
半圆内有一个直角三角形ABC,AB长为a厘米,AC长为b厘米,半圆的半径为r厘米,解答下面各题: 如图,在⊙O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,且AD=DC,求∠ABD的度数.
如图,在⊙O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,且AD=DC,求∠ABD的度数.