题目内容
12.先化简,再求值($\frac{a-1}{{a}^{2}+a-6}$+$\frac{a+2}{2a-{a}^{2}}$)÷$\frac{a+1}{{a}^{2}+3a}$-$\frac{2a+5}{4-{a}^{2}}$,其中a=-3.分析 首先把括号内的分式进行通分相减,把除法转化为乘法,然后进行分式的减法运算即可化简,然后代入数值计算即可.
解答 解:原式=[$\frac{a-1}{(a+3)(a-2)}+\frac{a-2}{a(2-a)}$]•$\frac{a(a+3)}{a+1}+\frac{2a+5}{(a+2)(a-2)}$
=$\frac{{a}^{2}-a-{a}^{2}-5a-6}{a(a+3)(a-2)}$•$\frac{a(a+3)}{a+1}$+$\frac{2a+5}{(a+2)(a-2)}$
=$\frac{-6}{a-2}$+$\frac{2a+5}{(a+2)(a-2)}$
=$\frac{-4a-7}{(a+2)(a-2)}$
=-$\frac{4a+7}{{a}^{2}-4}$.
当a=-3时,原式=-$\frac{4×(-3)+7}{{{{(-3)}^2}-4}}=-\frac{-5}{5}$=1
点评 本题考查了分式的化简求值,分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
7.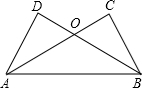 如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
 如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ②③ |
17.三角形中至少有一个角大于或等于( )
| A. | 30° | B. | 60° | C. | 70° | D. | 80° |
4.下列各式从左至右属于因式分解的是( )
| A. | x2-9+8x=(x+3)(x-3)+8x | B. | (x+3)(x-3)+8x=x2-9+8x | ||
| C. | (a+b)(a-b)=a2-b2 | D. | a2-2a(b-c)-3(b-c)2=(a-3b+3c)(a+b-c) |
1.下列长度的3根小棒,能搭成三角形的是( )
| A. | 9,5,2 | B. | 5,4,9 | C. | 4,6,9 | D. | 8,5,13 |
 已知:如图,△ABC中,D为AB的中点,E为AC上一点,连结ED并延长到点F,使DF=DE.求证:AC∥FB.
已知:如图,△ABC中,D为AB的中点,E为AC上一点,连结ED并延长到点F,使DF=DE.求证:AC∥FB.