题目内容
16.已知$\frac{a}{b}$=$\frac{1}{5}$,分式$\frac{a+b}{3a-7b}$的值为$-\frac{3}{16}$.分析 由$\frac{a}{b}$=$\frac{1}{5}$得到b=5a,然后代入计算即可.
解答 解:∵$\frac{a}{b}$=$\frac{1}{5}$,
∴b=5a.
∴原式=$\frac{a+5a}{3a-7×5a}$=$\frac{6a}{3a-35a}=\frac{6a}{-32a}$=$-\frac{3}{16}$.
故答案为:$-\frac{3}{16}$.
点评 本题主要考查的是分式的值,求得b=5a是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
1.设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的圆的圆心O在直线l上运动,A、O两点之间的距离为d.
(1)如图①,当r<a时,填表:
(2)如图②,⊙O与正方形有5个公共点B、C、D、E、F,求此时r与a之间的数量关系.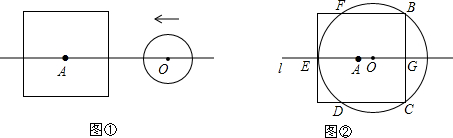
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
(1)如图①,当r<a时,填表:
| d,a,r之间的关系 | ⊙O与正方形的公共点个数 |
| d>a+r | 0 |
| d=a+r | 1 |
| a-r<d<a+r | 2 |
| d=a-r | 1 |
| 0≤d<a-r | 0 |
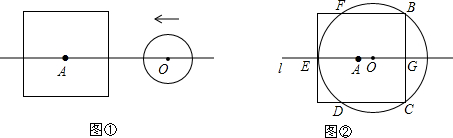
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
8.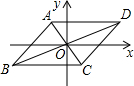 如图所示,已知平行四边形ABCD的两条对角线AC与BD交于平面直角坐标系的原点,点D的坐标为(3,2),则点B的坐标为( )
如图所示,已知平行四边形ABCD的两条对角线AC与BD交于平面直角坐标系的原点,点D的坐标为(3,2),则点B的坐标为( )
 如图所示,已知平行四边形ABCD的两条对角线AC与BD交于平面直角坐标系的原点,点D的坐标为(3,2),则点B的坐标为( )
如图所示,已知平行四边形ABCD的两条对角线AC与BD交于平面直角坐标系的原点,点D的坐标为(3,2),则点B的坐标为( )| A. | (-2,-3) | B. | (-3,2) | C. | (3,-2) | D. | (-3,-2) |
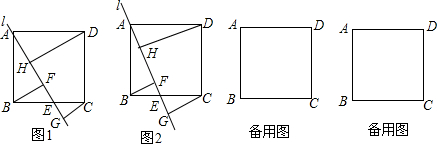
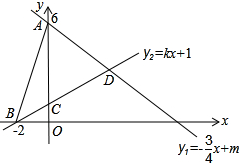 已知如图,直线${l_1}:{y_1}=-\frac{3}{4}x+m$与y轴交于A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求:
已知如图,直线${l_1}:{y_1}=-\frac{3}{4}x+m$与y轴交于A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求: