题目内容
4．函数y=2x+1的图象与函数y=x2-2x+6的图象交点的个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 根据联立，可得关于x的一元二次方程，根据根的判别式，可得答案．
解答 解：联立一次函数与二次函数，得
$\left\{\begin{array}{l}{y=2x+1}\\{y={x}^{2}-2x+6}\end{array}\right.$，
化简，得
x2-4x+5=0，
a=1，b=-4，c=5，
△=b2-4ac=（-4）2-4×1×5=-4＜0，
一元二次方程无解，
即y=2x+1的图象与函数y=x2-2x+6的图象交点的个数为0，
故选：A．
点评 本题考查了二次函数的性质，利用根的判别式：△=b2-4ac=（-4）2-4×1×5=-4＜0方程无解是解题关键．
练习册系列答案
相关题目
15．下列可以表示y为自变量x的函数的是（ ）
| A． | f（x）=$\sqrt{x-2}$+$\frac{1}{\sqrt{1-x}}$ | B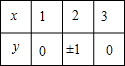． |  | C． |  | D． | y=1，x∈R |
如图，已知∠AOC在∠AOB的内部，∠AOB与∠AOC互为补角，OM平分∠AOC，ON平分∠BOM，若∠NOC=40°，求∠AOB的度数．
如图，在⊙O中，AB=2CD，求证：$\widehat{AB}$＞2$\widehat{CD}$．