题目内容
16. 如图所示,已知C,D将线段AB分成3:4:5三部分,E,F分别为AC,BD的中点,若EF=20.求AB的长.
如图所示,已知C,D将线段AB分成3:4:5三部分,E,F分别为AC,BD的中点,若EF=20.求AB的长.
分析 因为E、F分别是线段AB、CD的中点,故EF=CD+$\frac{1}{2}$(AC+DB)可求.
解答 解:∵C,D将线段AB分成3:4:5三部分,
∴AC=$\frac{3}{3+4+5}=\frac{1}{4}AB$,$CD=\frac{4}{3+4+5}=\frac{1}{3}AB$,$DB=\frac{5}{3+4+5}=\frac{5}{12}$AB;
∴EF=CD+$\frac{1}{2}$(AC+DB)=$\frac{1}{3}AB+\frac{1}{2}×(\frac{1}{4}AB+\frac{5}{12}AB)$=20
∴AB=30..
点评 此题考查两点间的距离问题,在一条直线或线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,最好准确画出几何图形,再根据题意进行计算.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
7.下列一元二次方程没有实数根的方程是( )
| A. | x2-1+x=0 | B. | 2x2+3x+2=0 | C. | 4x2+4x+1=0 | D. | x2-6x=9 |
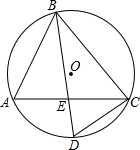 如图,△ABC内接于⊙O,D为$\widehat{AC}$的中点,BD交AC于点E.
如图,△ABC内接于⊙O,D为$\widehat{AC}$的中点,BD交AC于点E. 如图.已知:AB=6cm,BC=$\frac{1}{2}$AB,D为AC的中点,求DB的长.
如图.已知:AB=6cm,BC=$\frac{1}{2}$AB,D为AC的中点,求DB的长.