题目内容
17.先化简再求值:(1)2(x-3)-3(1+x-x2)-2($\frac{3}{2}$x2-2x),其中x=-$\frac{2}{3}$
(2)5(x+y)-4(3x-2y)+3(2x-3y),其中x是绝对值最小的数,y是最大的负整数.
分析 (1)原式去括号后合并得到最简结果,将x的值代入计算即可求出值.
(2)先根据绝对值的性质,负整数的定义得到x与y的值,原式去括号后合并得到最简结果,将x与y的值代入计算即可求出值.
解答 解:(1)2(x-3)-3(1+x-x2)-2($\frac{3}{2}$x2-2x)
=2x-6-3-3x+3x2-3x2+4x
=3x-9,
当x=-$\frac{2}{3}$时,原式=-2-9=-11;
(2)由题意得:x=0,y=-1,
原式=5x+5y-12x+8y+6x-9y
=-x+4y
=0-4
=-4.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
9.下列各式中无意义的式子是( )
| A. | -$\sqrt{5}$ | B. | ±$\sqrt{5}$ | C. | $\sqrt{-5}$ | D. | $\sqrt{(-5)^{2}}$ |
6. 如图,△ABC中,AB=AC,点D在AC边上,若AD=BD=BC,则∠A的度数为( )
如图,△ABC中,AB=AC,点D在AC边上,若AD=BD=BC,则∠A的度数为( )
 如图,△ABC中,AB=AC,点D在AC边上,若AD=BD=BC,则∠A的度数为( )
如图,△ABC中,AB=AC,点D在AC边上,若AD=BD=BC,则∠A的度数为( )| A. | 70° | B. | 45° | C. | 36° | D. | 30° |
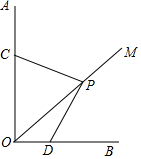 已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.PC和PD有怎样的数量关系,证明你的结论.
已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.PC和PD有怎样的数量关系,证明你的结论. △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.