题目内容
1.某物流公司的快递车和货车每天都从A地出发,往返于相距200千米的A,B两地,快递车比货车多往返一趟.快递车早8时出发,下午4时返回.已知货车每天只能往返一趟,且比快递车早1小时出发,到达B地后用2小时装卸货物,然后按原路、原速返回,结果比快递车最后一次返回A地晚1小时.(快递车在A、B两地停留时间忽略不计)(1)①快递车速度为50千米/时;
②两车在途中共相遇4次;
(2)求两车最后一次相遇时,距离A地的路程和货车从A地出发了几小时.
分析 (1)①设快递车的速度为x千米/小时,根据速度×时间=路程列出方程解答即可;
②求得货车速度,利用追击与相遇两个方面分析得出答案即可;
(2)求得最后一次相遇时间,得出答案即可.
解答 解:(1)①设快递车的速度为x千米/小时,由题意得
(16-8)x=200×2
解得x=50
答:快递车的速度为50千米/小时.
②货车速度:200×2÷(18-2)=25千米/小时,
第一次相遇:25÷(50-25)+8=9时,
第二次相遇:(200-5×25)÷(25+50)+4+8=13时,
第三次相遇:﹛200-[(1×2+2)×50-(4-1)×50]﹜÷(25+50)+13时=15时,
第四次相遇:(2×1/2)×25÷(50-25)+15时+1时=17时;
答:两车在途中共相遇4次
(2)货车出发了:17-7=10小时.
答:最后一次相遇货车从A地出发了10小时.
点评 此题考查一元一次方程的实际运用,掌握行程问题中的基本数量关系是解决问题的管家按.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
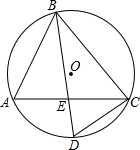 如图,△ABC内接于⊙O,D为$\widehat{AC}$的中点,BD交AC于点E.
如图,△ABC内接于⊙O,D为$\widehat{AC}$的中点,BD交AC于点E.