Question

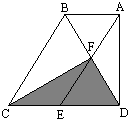如图，ABCE是一个平行四边形，ADE是一个直角三角形，它们组合成了梯形ABCD．如果这个梯形的上底、下底和高分别为2cm、5cm和4cm，则图中阴影部分的面积是

6

cm²．

Answer 1

分析：根据题干分析可得，AB=CE=2厘米，CD=5厘米，AD=4厘米，要求阴影部分的面积，只要求得三角形BCD的面积和DF与BD的比，利用高一定时，三角形的面积与底成正比的性质即可解答．

解答：解：AB=CE=2厘米，CD=5厘米，则DE=5-2=3厘米，
因为AB∥CD，所以DF：FB=DE：AB=3：2，
则DF：BD=3：5，
所以三角形CFD的面积：三角形BCD的面积=3：5，
三角形BCD的面积为：5×4÷2=10（平方厘米），
所以三角形CFD的面积为：10×3÷5=6（平方厘米），
答：阴影部分的面积是6平方厘米．
故答案为：6．

点评：此题考查了高一定时，三角形的面积与底成正比的灵活应用，根据题干得出相应的线段的长度是解决本题的关键．