题目内容
如图，梯形的高是10厘米，∠1=45°，则梯形的面积是多少平方厘米？
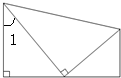
分析：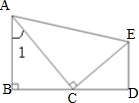
如图：∠1=45°，则∠ACB=45°，所以AB=BC；
因为∠ACE=90°，所以∠ECD=180°-90°-45°=45°，则∠DEC=45°，所以DE=CD；
根据：梯形的面积=（上底+下底）×高÷2可得：（DE+AB）×10÷2，因为AB=BC，DE=CD，所以DE+AB=BC+CD=10，由此代入，解答即可．
如图：∠1=45°，则∠ACB=45°，所以AB=BC；因为∠ACE=90°，所以∠ECD=180°-90°-45°=45°，则∠DEC=45°，所以DE=CD；
根据：梯形的面积=（上底+下底）×高÷2可得：（DE+AB）×10÷2，因为AB=BC，DE=CD，所以DE+AB=BC+CD=10，由此代入，解答即可．
解答：解：如图：：∠1=45°，则∠ACB=45°，所以AB=BC；
因为∠ACE=90°，所以∠ECD=180°-90°-45°=45°，则∠DEC=45°，所以DE=CD；
根据：梯形的面积=（上底+下底）×高÷2可得：
（DE+AB）×10÷2
=（BC+CD）×10÷2
=10×10÷2
=50（平方厘米）；
答：梯形的面积是50平方厘米．
如图：：∠1=45°，则∠ACB=45°，所以AB=BC；因为∠ACE=90°，所以∠ECD=180°-90°-45°=45°，则∠DEC=45°，所以DE=CD；
根据：梯形的面积=（上底+下底）×高÷2可得：
（DE+AB）×10÷2
=（BC+CD）×10÷2
=10×10÷2
=50（平方厘米）；
答：梯形的面积是50平方厘米．
点评：此题考查了梯形面积计算公式的应用，根据题意，推导出DE+AB=BC+CD=10，是解答此题的关键．
练习册系列答案
相关题目
如图：在一个梯形的果园上铺一条平行四边形小路，小路的底是3米，高是10米，每3平方米种植一棵果树，这块地共种多少棵果树？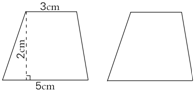
用如图两个完全一样的梯形拼成一个平行四边形．拼成的平行四边形的高是2厘米，底是多少厘米？（ ）
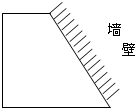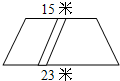
如图，用篱笆围成一块梯形菜地，它的一边是利用了屋子的墙壁，篱笆长50米，梯形高是10米，这块梯形菜地的面积为（ ）平方米．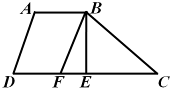
如图，梯形ABCD中，上底AB的长度是10厘米，梯形的高BE的长度是12厘米，且E是CD中点，BF将梯形ABCD分成面积相等的两部分．那么，EF的长度是