题目内容
将一块体积为200立方分米的正方体木块,加工成最大圆柱,圆柱体积为
157
157
立方分米.分析:将一块体积为200立方分米的正方体木块,加工成最大圆柱,那么这个圆柱的底面直径应该是正方体的边长a分米,高也应该是正方体的边长a分米,正方体的体积=a3,
长方体体积=πr2h,再根据圆柱的体积与正方体的积之间的关系.解答即可.
长方体体积=πr2h,再根据圆柱的体积与正方体的积之间的关系.解答即可.
解答:解:设正方体的棱长为a分米,
正方体的体积=a×a×a=a3=200(立方分米),
圆柱的体积=πr2h=3.14×(a÷2)×a2×a,
=3.14×
×a,
=
a3,
=
×200,
=3.14×50,
=157(立方分米);
答:圆柱的体积是157立方分米.
正方体的体积=a×a×a=a3=200(立方分米),
圆柱的体积=πr2h=3.14×(a÷2)×a2×a,
=3.14×
| a2 |
| 4 |
=
| 3.14 |
| 4 |
=
| 3.14 |
| 4 |
=3.14×50,
=157(立方分米);
答:圆柱的体积是157立方分米.
点评:此题考查了学生的空间相象能力,怎样从正方体中得到一个最大的圆柱体,必须使圆柱的底面直径和高与正方体边长相等,再利用长方体和正方体公式进行灵活运用即可求出.

练习册系列答案
相关题目
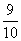 。小明将一块体积为0.8立方分米的铁块放入水中,经测量发现水面上升了2厘米,水槽正好装满。制作这个玻璃水槽需要多少玻璃?(玻璃厚度和接口忽略不计)
。小明将一块体积为0.8立方分米的铁块放入水中,经测量发现水面上升了2厘米,水槽正好装满。制作这个玻璃水槽需要多少玻璃?(玻璃厚度和接口忽略不计)