题目内容
用一张长40厘米、宽是20厘米的长方形硬纸,围成一个容积最大的圆柱体,该怎样围?容积是多少?
解:方法一:以40厘米为高,20厘米为底面周长,
则底面半径是:20÷π÷2=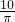 (厘米),
(厘米),
容积是:π× ×40=
×40= (立方厘米),
(立方厘米),
方法二:以20厘米为高,40厘米为底面周长,
则底面半径是:40÷π÷2=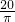 (厘米),
(厘米),
容积是:π× ×20=
×20= (立方厘米),
(立方厘米),
由上述计算可得:以20厘米为高,40厘米为底面周长,围成的圆柱体的容积最大,是 立方厘米.
立方厘米.
分析:根据题干分析可得,有两种不同的围法:一种是以40厘米为高,20厘米为底面周长,另一种是以20厘米为高,40厘米为底面周长,据此利用圆柱的容积公式求出它们的容积即可解答.
点评:根据圆柱的侧面展开图的特征,得出这两种不同的围成方法,是解决本题的关键.
则底面半径是:20÷π÷2=
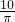 (厘米),
(厘米),容积是:π×
 ×40=
×40= (立方厘米),
(立方厘米),方法二:以20厘米为高,40厘米为底面周长,
则底面半径是:40÷π÷2=
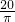 (厘米),
(厘米),容积是:π×
 ×20=
×20= (立方厘米),
(立方厘米),由上述计算可得:以20厘米为高,40厘米为底面周长,围成的圆柱体的容积最大,是
 立方厘米.
立方厘米.分析:根据题干分析可得,有两种不同的围法:一种是以40厘米为高,20厘米为底面周长,另一种是以20厘米为高,40厘米为底面周长,据此利用圆柱的容积公式求出它们的容积即可解答.
点评:根据圆柱的侧面展开图的特征,得出这两种不同的围成方法,是解决本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目