题目内容
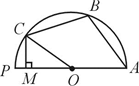 如图,一个半圆的圆心为O,一束光由点M沿垂直于PA的方向射向半圆,光线在圆周上的点C处反射,反射角∠OCB等于入射角∠MCO;接着这束光再与圆周交于点B,依同样方式反射,最后光射入点A,则∠COM=
如图,一个半圆的圆心为O,一束光由点M沿垂直于PA的方向射向半圆,光线在圆周上的点C处反射,反射角∠OCB等于入射角∠MCO;接着这束光再与圆周交于点B,依同样方式反射,最后光射入点A,则∠COM=36°
36°
.分析:如图,过点O作BC的垂线OD,因为∠OCB=∠MCO,根据角的平分线的性质可得OD=OM,则三角形COM与三角形COD是全等三角形,则可得∠COM=∠1,同理,反射角∠ABO=入射角∠CBO,可推得∠2=∠4;又因为OC=OB=OA,不难得出∠1=∠2,∠3=∠4;据此可得:∠COM=∠1=∠2=∠3=∠4,又因为这五个角的和是平角180°,据此即可求出∠COM的度数.
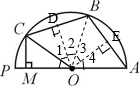

解答:解:连接OB,且过点O作BC的垂线OD,作AB的垂线段OE,
因为∠OCB=∠MCO,根据角的平分线的性质可得OD=OM,
则三角形COM与三角形COD是全等三角形,
则∠COM=∠1,
同理,如图,反射角∠ABO=入射角∠CBO,
可推得∠2=∠4;
又因为OC=OB=OA,不难得出∠1=∠2,∠3=∠4;
所以:∠COM=∠1=∠2=∠3=∠4,
又因为这五个角的和是平角180°,
所以∠COM=180°÷5=36°.
答:∠COM=36°.
故答案为:36°.
因为∠OCB=∠MCO,根据角的平分线的性质可得OD=OM,
则三角形COM与三角形COD是全等三角形,
则∠COM=∠1,
同理,如图,反射角∠ABO=入射角∠CBO,
可推得∠2=∠4;
又因为OC=OB=OA,不难得出∠1=∠2,∠3=∠4;
所以:∠COM=∠1=∠2=∠3=∠4,
又因为这五个角的和是平角180°,
所以∠COM=180°÷5=36°.
答:∠COM=36°.
故答案为:36°.
点评:解答此题的关键是明确两次反射与折射时,反射角=折射角,再利用圆内的等腰三角形及全等三角形的性质即可解答问题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图中每个小方格的边长都是1厘米
如图中每个小方格的边长都是1厘米

