Question

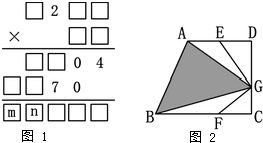
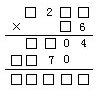
有一个算式，式中画的“×”表示缺掉的数字，求除数的所有不同的质因数的和=

9

．

Answer 1

分析：由除数与8的积是三位数，而个位上的商与除数的积是四位数可以得出：个位上的数字是9，由此即可进行推理解决．

解答：解：根据题意可得，
因为8乘以这个数得到的是三位数，可以得到除数首位只能是1，
因为商8后的余数是三位数，所以8与除数的乘积的首位必定是8，从而9-8=1．所以余数的首位数字是1，
那么，除数的第二位也就出来了，也是1，因为只要大于二就要进位，乘积首位就变成9或其他．
所以这个除数百位和十位上的数字都是1，应该是11□．
由除数与8的积是三位数，而个位上的商与除数的积是四位数可以得出：商的个位上的数字是9，
同时也可得知除数最后一位必然不是1，因为9×111=999是三位数．
这样一来，再根据8×11□是三位数且首位为8，那么□里的数字只能是2了．除数就只能是112了．
112=2×2×2×2×7，
2+7=9，
答：除数的所有不同的质因数的和是9，
故答案为：9．

点评：此题的突破口在于商中的8．