题目内容
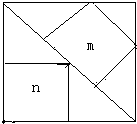 如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求
如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求 的值?
的值?
解:如图所示,

(1)因为S△BEF=S△AEF,S△BEG=S△CEG,
所以S1= ×S△ABC,
×S△ABC,
又因S△JHK=S△JAK S△HIJ=S△CIH,
则S2= ×梯形HIJK,
×梯形HIJK,
又因S△ABC=S△ADC>S梯形HIJK,
所以S1>S2,即n>m;
(2)面积为n的正方形旁边是直角三角形,因为其斜边是正方形对角线,
所以那个角是45度,所以它是个等腰直角三角形,
可得此正方形的边长为大正方形边长的一半,
设大正方形的边长是1,则此正方形边长为 ,则n=
,则n= ;
;
同理 面积为m的正方形两边也是等腰直角三角形,
所以此正方形边长为大正方形对角线长的 ,
,
即此正方形边长为 ×
× ,所以m=
,所以m=
所以 =
=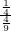 =
= ;
;
答:n的面积比m的大, =
= ;
;
分析:如图所示,分别得出两个正方形的面积与大正方形的面积的关系,即可比较出它们的大小;设出大正方形的边长,求出两个小正方形的边长,进而利用正方形的面积公式即可求解.
点评:此题有些难度,需要灵活利用正方形的面积公式,关键是得出它们的面积与正方形的面积的关系.

(1)因为S△BEF=S△AEF,S△BEG=S△CEG,
所以S1=
 ×S△ABC,
×S△ABC,又因S△JHK=S△JAK S△HIJ=S△CIH,
则S2=
 ×梯形HIJK,
×梯形HIJK,又因S△ABC=S△ADC>S梯形HIJK,
所以S1>S2,即n>m;
(2)面积为n的正方形旁边是直角三角形,因为其斜边是正方形对角线,
所以那个角是45度,所以它是个等腰直角三角形,
可得此正方形的边长为大正方形边长的一半,
设大正方形的边长是1,则此正方形边长为
 ,则n=
,则n= ;
;同理 面积为m的正方形两边也是等腰直角三角形,
所以此正方形边长为大正方形对角线长的
 ,
,即此正方形边长为
 ×
× ,所以m=
,所以m=
所以
 =
=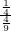 =
= ;
;答:n的面积比m的大,
 =
= ;
;分析:如图所示,分别得出两个正方形的面积与大正方形的面积的关系,即可比较出它们的大小;设出大正方形的边长,求出两个小正方形的边长,进而利用正方形的面积公式即可求解.
点评:此题有些难度,需要灵活利用正方形的面积公式,关键是得出它们的面积与正方形的面积的关系.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求
如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求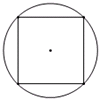 如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为:
如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为: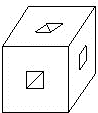 如图所示,有一个边长为5厘米的立方体木块,在它的每个角以及每条棱和每个面的中间各挖去一个边长为1厘米的小立方体(即图中画有阴影的那些小立方体),那么余下部分的表面积是多少平方厘米?
如图所示,有一个边长为5厘米的立方体木块,在它的每个角以及每条棱和每个面的中间各挖去一个边长为1厘米的小立方体(即图中画有阴影的那些小立方体),那么余下部分的表面积是多少平方厘米? 如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为:________(结果可以含有π)
如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为:________(结果可以含有π)