题目内容
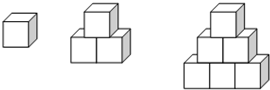
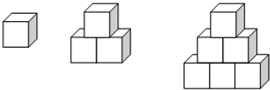
先观察、分析如图所示各组摆放情况,再填表格(注:每个小正方体棱长1厘米)
| 层数 | 1 | 2 | 3 | … | 5 | … |
| 正方体个数 | 1 | 3 | 6 | … | … | |
| 图形表面积(平方厘米) | 6 | 14 | 24 | … | … | |
| 图形体积(立方厘米) | 1 | 3 | 6 | … | … |
解:(1)第一个图形有:1个小正方体,;第二个图形有:1+2=3个小正方体;第三个图形有:1+2+3个小正方体;第四个图形有:1+2+3+4=10个小正方体,…由此可得第n个图形有:1+2+3+…+n个小正方体;
(2)第一个图形的表面积是1×4+1×2=6;第二个图形的表面积是:2×4+3×2=14;第三个图形的表面积是:3×4+6×2=24;第四个图形的表面积是:4×4+10×2=36…如果第n个图形中的小正方体的个数用a表示,所以第n个图形的表面积就是4n+2a.
(3)每个图形的体积与组成它的小正方体的个数数量相等.
由上述推理得出的结论即可完成上表如下
分析:(1)观察图形可知,图形的排列特点是按照小正方体的个数排列为:1、1+2、1+2+3、1+2+3+4+…;
(2)每个图形的表面积与组成它的小正方体的个数有关,根据已知的图形推理出一般结论即可解答;
(3)每一个图形中的体积数与小正方体的个数数量相同;
点评:观察题干,由已知的图形排列特点,得出每个图形中小正方体的个数、表面积、体积之间的关系是解决本题的关键.
(2)第一个图形的表面积是1×4+1×2=6;第二个图形的表面积是:2×4+3×2=14;第三个图形的表面积是:3×4+6×2=24;第四个图形的表面积是:4×4+10×2=36…如果第n个图形中的小正方体的个数用a表示,所以第n个图形的表面积就是4n+2a.
(3)每个图形的体积与组成它的小正方体的个数数量相等.
由上述推理得出的结论即可完成上表如下
| 层数 | 1 | 2 | 3 | … | 5 | … |
| 正方体个数 | 1 | 3 | 6 | … | 15 | … |
| 图形表面积(平方厘米) | 6 | 14 | 24 | … | 50 | … |
| 图形体积(立方厘米) | 1 | 3 | 6 | … | 15 | … |
分析:(1)观察图形可知,图形的排列特点是按照小正方体的个数排列为:1、1+2、1+2+3、1+2+3+4+…;
(2)每个图形的表面积与组成它的小正方体的个数有关,根据已知的图形推理出一般结论即可解答;
(3)每一个图形中的体积数与小正方体的个数数量相同;
点评:观察题干,由已知的图形排列特点,得出每个图形中小正方体的个数、表面积、体积之间的关系是解决本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目