题目内容
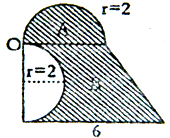如图是由图形A和图形B两部分拼成的组合图形．如果将阴影部分的半圆A绕点O________时针旋转________度后可与图形B组合成一个梯形，那么梯形（阴影部分）的面积是多少平方米？
顺 90
分析：由题意可知：如果将阴影部分的半圆A绕点O顺时针旋转90度后可与图形B组合成一个梯形，梯形的上底和高都等于半圆的直径，下底已知，于是利用梯形的面积公式即可求解．
解答：如果将阴影部分的半圆A绕点O顺时针旋转90度后可与图形B组合成一个梯形，
其面积为：（2×2+6）×（2×2）÷2，
=10×4÷2，
=40÷2，
=20（平方米）；
答：梯形的面积是20平方米．
故答案为：顺、90．
点评：此题主要考查梯形的面积的计算方法，关键是明白：梯形的上底和高都等于半圆的直径．
分析：由题意可知：如果将阴影部分的半圆A绕点O顺时针旋转90度后可与图形B组合成一个梯形，梯形的上底和高都等于半圆的直径，下底已知，于是利用梯形的面积公式即可求解．
解答：如果将阴影部分的半圆A绕点O顺时针旋转90度后可与图形B组合成一个梯形，
其面积为：（2×2+6）×（2×2）÷2，
=10×4÷2，
=40÷2，
=20（平方米）；
答：梯形的面积是20平方米．
故答案为：顺、90．
点评：此题主要考查梯形的面积的计算方法，关键是明白：梯形的上底和高都等于半圆的直径．
练习册系列答案
相关题目
如图是由一个正三角形和三个正方形拼成的轴对称图形，它有多少条对称轴（ ）
如图是一个由两个正方形拼合而成的图形，它们的边长分别是m厘米及n厘米，且CDE为一直线．已知m和n都是两位数，且m2=2n．若三角形ABC的面积等于a平方厘米，求a的最大值．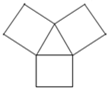
如图是由一个正三角形和三个正方形拼成的轴对称图形它有都是挑对称轴