题目内容
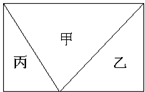 把一个长方形分成甲、乙、丙三个三角形,甲比乙的面积大20平方厘米,乙与丙的面积比是3:2,则原来这个长方形的面积是
把一个长方形分成甲、乙、丙三个三角形,甲比乙的面积大20平方厘米,乙与丙的面积比是3:2,则原来这个长方形的面积是100
100
平方厘米.分析:由图意可知:甲的面积=乙的面积+丙的面积,甲比乙多的部分就是丙的面积,丙的面积就是20平方厘米,由此可以求出乙的面积,进而可求出长方形的面积.
解答:解:乙与丙的面积比是3:2,也就是乙的面积是丙的
,
(20+20×
)×2,
=(20+30)×2,
=50×2,
=100(平方厘米);
答:原来长方形的面积是100平方厘米.
故答案为:100.
| 3 |
| 2 |
(20+20×
| 3 |
| 2 |
=(20+30)×2,
=50×2,
=100(平方厘米);
答:原来长方形的面积是100平方厘米.
故答案为:100.
点评:此题主要考查等底等高的图形面积大小及比的意义,将数据代入公式即可求得结果.

练习册系列答案
相关题目
 如图所示,把一个正方形分成四个长方形,正方形周长与甲乙丙丁四个长方形周长之和的比是
如图所示,把一个正方形分成四个长方形,正方形周长与甲乙丙丁四个长方形周长之和的比是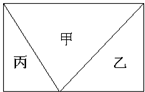 把一个长方形分成甲、乙、丙三个三角形,甲比乙的面积大20平方厘米,乙与丙的面积比是3:2,则原来这个长方形的面积是________平方厘米.
把一个长方形分成甲、乙、丙三个三角形,甲比乙的面积大20平方厘米,乙与丙的面积比是3:2,则原来这个长方形的面积是________平方厘米.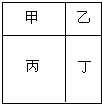 如图所示,把一个正方形分成四个长方形,正方形周长与甲乙丙丁四个长方形周长之和的比是________.
如图所示,把一个正方形分成四个长方形,正方形周长与甲乙丙丁四个长方形周长之和的比是________.