题目内容
操作与计算.
(1)在右面的空白处画一个周长为12.56厘米的圆,并在圆内画两条相互垂直的直径,然后依次连接这两条直径的四个端点,得到一个正方形,这个正方形的面积是________平方厘米.
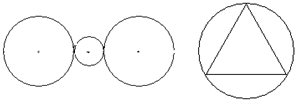
(2)画出如图的对称轴.(有几条画几条)
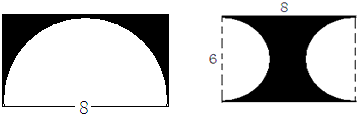
(3)求各图阴影部分的面积.(单位:dm)
解:(1)由题意知,周长为12.56厘米的圆的半径为:
12.56÷π÷2,
=12.56÷3.14÷2,
=2(厘米);
半径为2厘米的圆如下图所示:
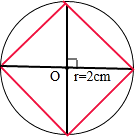
正方形的面积为:4×(2×2÷2)=8(平方厘米);
答:这个正方形的面积是8平方厘米.
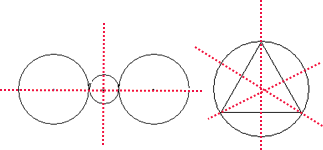
(2)据分析画图形的对称轴如下所示:
(3)左边图形中阴影部分的面积为:
8×(8÷2)-3.14×(8÷2)2÷2,
=32-3.14×16÷2,
=32-25.12,
=6.88(平方厘米);
右边图形中阴影部分的面积是:
8×6-3.14×(6÷2)2,
=48-3.14×9,
=48-28.26,
=19.74(平方厘米);
答:阴影部分的面积分别为6.88平方厘米和19.74平方厘米.
故答案为:8.
分析:(1)先根据圆的周长求出圆的半径,由半径画出我们所需的圆,然后画两条相互垂直的直径,最后依次连接这两条直径的四个端点,得到一个正方形,再根据圆的内接四边形和小三角形的关系求出正方形的面积来.
(2)依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此即可进行解答.
(3)左边图形中阴影部分的面积=长方形的面积-半圆的面积,又因长方形的长等于半圆的直径,宽等于半圆的半径;右边图形中阴影部分的面积=长方形的面积-圆的面积,圆的直径等于长方形的宽,于是利用长方形和圆的面积公式即可求解.
点评:(1)此题考查了根据圆的周长求圆的半径,并考查了学生的作图能力,以及如何根据图求圆内接正方形的面积.
(2)解答此题的主要依据是轴对称图形的意义.
(3)解答此题的关键是弄清楚长方形的长和宽与圆的直径和半径的关系,问题即可得解.
12.56÷π÷2,
=12.56÷3.14÷2,
=2(厘米);
半径为2厘米的圆如下图所示:

正方形的面积为:4×(2×2÷2)=8(平方厘米);
答:这个正方形的面积是8平方厘米.
(2)据分析画图形的对称轴如下所示:

(3)左边图形中阴影部分的面积为:
8×(8÷2)-3.14×(8÷2)2÷2,
=32-3.14×16÷2,
=32-25.12,
=6.88(平方厘米);
右边图形中阴影部分的面积是:
8×6-3.14×(6÷2)2,
=48-3.14×9,
=48-28.26,
=19.74(平方厘米);
答:阴影部分的面积分别为6.88平方厘米和19.74平方厘米.
故答案为:8.
分析:(1)先根据圆的周长求出圆的半径,由半径画出我们所需的圆,然后画两条相互垂直的直径,最后依次连接这两条直径的四个端点,得到一个正方形,再根据圆的内接四边形和小三角形的关系求出正方形的面积来.
(2)依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此即可进行解答.
(3)左边图形中阴影部分的面积=长方形的面积-半圆的面积,又因长方形的长等于半圆的直径,宽等于半圆的半径;右边图形中阴影部分的面积=长方形的面积-圆的面积,圆的直径等于长方形的宽,于是利用长方形和圆的面积公式即可求解.
点评:(1)此题考查了根据圆的周长求圆的半径,并考查了学生的作图能力,以及如何根据图求圆内接正方形的面积.
(2)解答此题的主要依据是轴对称图形的意义.
(3)解答此题的关键是弄清楚长方形的长和宽与圆的直径和半径的关系,问题即可得解.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 操作与计算
操作与计算

 实际操作与计算.
实际操作与计算. 操作与计算
操作与计算