题目内容
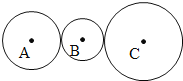
【题目】如图是A、B、C三个互相的咬合的齿轮.若A轮转3圈,B轮转7圈,C轮转2圈,那么这三个齿轮的齿数最少是A轮 齿,B轮 齿,C轮 齿.
【答案】14,6,21
【解析】
试题分析:由题意可知:若A轮转3圈,B轮转7圈,C轮转2圈三个齿轮转过的总齿数是相等的,即转过的总齿数是3、7、2的公倍数,要求最少,就是转过的总齿数是3、7、2的最小公倍数,然后用这三个数的最小公倍数分别除以它们的圈数就是各自的齿数.
解:3、7、2三个数两两互质,它们的最小公倍数是它们的乘积:3×7×2=42,
即三个齿轮转过的总齿数是42,
A为:42÷3=14(齿);
B:42÷7=6(齿);
C:42÷2=21(齿);
故答案为:14,6,21.

练习册系列答案
相关题目