题目内容
如图是一个正方形．
①画一个圆，使正方形的四个顶点都在圆上；
②正方形的面积约占圆面积的________%
64
分析：（1）以正方形的对角线的交点为圆心，以正方形的对角线的一半为半径，所画出的圆就是所要求画的圆．
（2）设圆的半径为r，分别利用正方形和圆的面积公式表示出二者的面积，于是就可以求出正方形的面积占圆的面积的百分之几．
解答：（1）据分析画圆如下：
；
（2）设圆的半径为r，
则正方形的面积为：2r×r÷2×2=2r2，
圆的面积为：πr2，
2r2÷πr2，
=2÷3.14，
≈0.64，
≈64%；
答：正方形的面积约占圆面积的64%．
故答案为：64．
点评：解答此题的关键是：让圆的半径等于正方形的对角线的一半，问题即可逐步得解．
分析：（1）以正方形的对角线的交点为圆心，以正方形的对角线的一半为半径，所画出的圆就是所要求画的圆．
（2）设圆的半径为r，分别利用正方形和圆的面积公式表示出二者的面积，于是就可以求出正方形的面积占圆的面积的百分之几．
解答：（1）据分析画圆如下：
；（2）设圆的半径为r，
则正方形的面积为：2r×r÷2×2=2r2，
圆的面积为：πr2，
2r2÷πr2，
=2÷3.14，
≈0.64，
≈64%；
答：正方形的面积约占圆面积的64%．
故答案为：64．
点评：解答此题的关键是：让圆的半径等于正方形的对角线的一半，问题即可逐步得解．
练习册系列答案
相关题目
如图是一个正方形的池塘，池塘中间有一个长方形的小岛．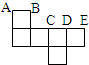
（2006?徐州）如图是一个正方形纸盒的展开图，当折叠成正方体纸盒时，C点与（ ）点重合．
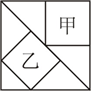（2012?江汉区模拟）如图是一个正方形，甲和乙分别是等腰三角形的两种不同的内接正方形，则图中甲与乙的面积比是
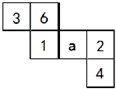如图是一个正方形的展开图，那么a对面的数字是
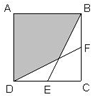如图是一个正方形，边长6厘米，E、F分别是CD、BC的中点，求阴影部分的面积．