题目内容
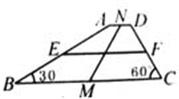如图所示，在四边形ABCD中，AD∥BC，角B=30度，角C等于60度，E、M、F、N分别为所在边的中点，已知BC=7，MN=3，求EF．分析：先延长BA、CD交与点P，则三角形PBC为直角三角形，MP为其斜边上的中线，利用直角三角形斜边中线与斜边的关系及梯形中位线的特点，即可求解．
解答：4解：如图所示，
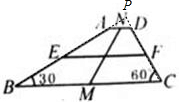
延长BA、CD交与点P，则三角形PBC为直角三角形，MP为其斜边上的中线，
于是NP也为直角三角形PAD斜边上的中线，MP=7÷2=3.5，NP=MP-MN=3.5-3=0.5，
AD=2×0.5=1；
EF为梯形的中位线，EF=（1+7）÷2=4．
答：EF为4．
延长BA、CD交与点P，则三角形PBC为直角三角形，MP为其斜边上的中线，
于是NP也为直角三角形PAD斜边上的中线，MP=7÷2=3.5，NP=MP-MN=3.5-3=0.5，
AD=2×0.5=1；
EF为梯形的中位线，EF=（1+7）÷2=4．
答：EF为4．
点评：此题关键是添加辅助线，利用直角三角形斜边中线与斜边的关系及梯形中位线的特点，即可求解．
练习册系列答案
相关题目
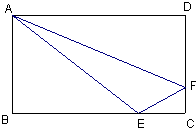如图所示，在长方形ABCD中，△ABE、△ADF和四边形AECF的面积都相等，且BE=8，则EC的长为（ ）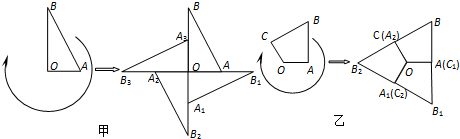
如图，把正方形ACFG与Rt△ACB按如图①所示重叠在一起，其中AC=2，∠BAC=60°，若把Rt△ACB绕直角顶点C按顺时针方向旋转，使斜边AB恰好经过正方形ACFG的顶点F，得△A′B′C，AB分别与A′C、A′B′相交于点D、E，如图②所示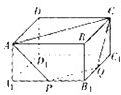
如图所示的是一个长方体，四边形APQC、是长方体的一个截面（即过长方体上4点A、P、Q、C的平面与长方体相交所得到的图形），P、Q分别为棱A1B1、B1C1，的中点，请在此长方体的平面展开图上，标出线段AC、cQ、QP、PA．