题目内容
 如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为:________(结果可以含有π)
如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为:________(结果可以含有π)

分析:由图形可知:正方形对角线等于圆的直径,正方形沿对角线平均分成两个完全一样的三角形,三角形的底等于圆的直径,三角形的高等于圆的半径,设圆的半径为r,根据三角形的面积公式:s=
 ah,已知正方形的边长为1,由此可以求出半径的平方,再根据圆的面积公式:s=πr2,即可求出圆的面积.
ah,已知正方形的边长为1,由此可以求出半径的平方,再根据圆的面积公式:s=πr2,即可求出圆的面积.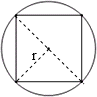
解答:设圆半径为r,则三角形的底为2r(直径),
正方形的面积为:
2r×r÷2×2=1×1,
2r×r=1,
r2=
 ,
,圆的面积=πr2=π×
 =
=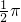 ,
,答:圆的面积是
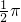 .
.故答案为:
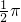 .
.点评:此题主要考查圆的面积计算,把正方形平均分成两个完全一样的三角形,找出三角形底和高圆的半径和直径的关系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有一个长方体形状的泡沫塑料,长、宽、高分别为4米、5米、6米,现沿水平方向按任意尺寸将它切成4片,再将每片按任意尺寸平行于6米边切成5条,每条又按任意尺寸平行于5米边切成6小块,问共得到大大小小的长方体多少块?它们的面积的总和是多少平方米?切法如图所示.
有一个长方体形状的泡沫塑料,长、宽、高分别为4米、5米、6米,现沿水平方向按任意尺寸将它切成4片,再将每片按任意尺寸平行于6米边切成5条,每条又按任意尺寸平行于5米边切成6小块,问共得到大大小小的长方体多少块?它们的面积的总和是多少平方米?切法如图所示.
 10、一个棱长为1的小正方体形状的骰子,它的六个面上各写有一个大写英文字母D、E、G、I、N、O中的一个.先将它放在由20个边长为1的小正方形拼成的4×5的棋盘的左上角的小方格上,令字母D朝上(如图所示),然后将它连续的向邻格翻动,并且恰好经过4×5棋盘上的其余的19个小方格各1次(共翻动了19次),最终停止在棋盘的右下角的小方格上.如果图中小方格中给定的字母是骰子在翻动到该小方格上时,骰子朝上的面上所写的字母(字母可“正放”、“横放”或“倒放”).那么,骰子翻动到画有“﹡”的小方格时,骰子朝上的面所写的字母是( )
10、一个棱长为1的小正方体形状的骰子,它的六个面上各写有一个大写英文字母D、E、G、I、N、O中的一个.先将它放在由20个边长为1的小正方形拼成的4×5的棋盘的左上角的小方格上,令字母D朝上(如图所示),然后将它连续的向邻格翻动,并且恰好经过4×5棋盘上的其余的19个小方格各1次(共翻动了19次),最终停止在棋盘的右下角的小方格上.如果图中小方格中给定的字母是骰子在翻动到该小方格上时,骰子朝上的面上所写的字母(字母可“正放”、“横放”或“倒放”).那么,骰子翻动到画有“﹡”的小方格时,骰子朝上的面所写的字母是( )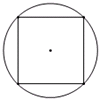 如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为:
如图所示,将一个边长为1的正方形嵌入一个圆中,使正方形的四个顶点都在圆上,则圆的面积为: