题目内容
图中ABCD 是直角梯形．其中AD=12厘米，AB=8厘米，BC=15厘米，且△ADE、四边行DEBF及△CDF的面积相等．三角形EBF（阴影部分）的面积是多少平方厘米？
解：又因三角形ADE和三角形CDF的面积S=（12+15）×8÷2÷3=36（平方厘米），
所以BE=8-36×2÷12=2（厘米），
BF=15-36×2÷8=6（厘米），
所以△EBF的面积为2×6÷2=6（平方厘米）；
答：阴影部分的面积是6平方厘米．
分析：可以根据已知条件，先求出FC和AE的长，再求得BF=15-FC，BE=8-AE，就可以计算出△EBF的面积，又因△ADE、四边行DEBF及△CDF的面积相等，则三角形ADE和三角形CDF的面积S=（12+15）×8÷2÷3=36（平方厘米），于是即可求出BE的长度，再据三角形的面积公式即可求解．
点评：解答此题的关键是：利用三角形的面积公式分别求出BF、BE的长度，问题即可得解．
所以BE=8-36×2÷12=2（厘米），
BF=15-36×2÷8=6（厘米），
所以△EBF的面积为2×6÷2=6（平方厘米）；
答：阴影部分的面积是6平方厘米．
分析：可以根据已知条件，先求出FC和AE的长，再求得BF=15-FC，BE=8-AE，就可以计算出△EBF的面积，又因△ADE、四边行DEBF及△CDF的面积相等，则三角形ADE和三角形CDF的面积S=（12+15）×8÷2÷3=36（平方厘米），于是即可求出BE的长度，再据三角形的面积公式即可求解．
点评：解答此题的关键是：利用三角形的面积公式分别求出BF、BE的长度，问题即可得解．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
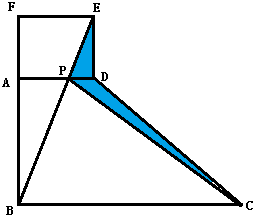如图，ABCD是个直角梯形（∠DAB=∠ABC=90°）．以AD为一边向外作长方形ADEF，其面积为6.36平方厘米，连接BE交AD于P，再连接PC．则图中阴影部分的面积是（ ）平方厘米．
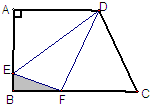图中ABCD 是直角梯形．其中AD=12厘米，AB=8厘米，BC=15厘米，且△ADE、四边行DEBF及△CDF的面积相等．三角形EBF（阴影部分）的面积是多少平方厘米？
