题目内容
计算.能简算的要简算.
| 25×1.25×32 | (3.75+4.1+2.35)×9.8 | 12×( + + - - ) ) |
| (20.2×0.4+7.88)÷4.2 | ( + + )÷ )÷ + + | 10÷[ -( -( ÷ ÷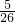 + + )]. )]. |
解:(1)25×1.25×32,
=(25×4)×(1.25×8),
=100×10,
=1000;
(2)(3.75+4.1+2.35)×9.8,
=[(3.75+2.35)+4.1]×9.8,
=[6.1+4.1]]×9.8,
=(10+0.2)×(10-0.2),
=100-0.04,
=99.96;
(3)12×( +
+ -
- ),
),
=12× +12×
+12× -12×
-12× ,
,
=3+2-4,
=1;
(5)( +
+ )÷
)÷ +
+ ,
,
= ×
× +
+ ,
,
= +
+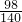 ,
,
=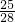 ;
;
(6)10÷[ -(
-( ÷
÷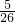 +
+ )],
)],
=10÷[ -(2+
-(2+ )]
)]
=10÷[ -
- ],
],
=10÷ ,
,
= .
.
分析:(1)25×1.25×32把32拆成4×8,利用乘法的结合律变成(25×4)×(1.25×8)计算简便;
(2)(3.75+4.1+2.35)×9.8把括号里的((3.75+4.1+2.35)变成[(3.75+2.35)+4.1]=6.1+4.1=10.2,再把9.8变成(10-0.2)平方差公式变成(10+0.2)×(10-0.2)计算;
(3)12×( +
+ -
- )利用乘法的结合律变成12×
)利用乘法的结合律变成12× +12×
+12× -12×
-12× 计算简便;
计算简便;
(4)(20.2×0.4+7.88)÷4.2利用四则运算的顺序,先算括号里的20.2×0.4再算括号里的加,最后算除;
(5)( +
+ )÷
)÷ +
+ 利用四则运算的顺序,先算括号里的加再算括号外的除,最后算加;
利用四则运算的顺序,先算括号里的加再算括号外的除,最后算加;
(6)10÷[ -(
-( ÷
÷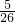 +
+ )]先算括号里的除再算括号里的加,然后算中括号里面的减法,最后算括号外面的除.
)]先算括号里的除再算括号里的加,然后算中括号里面的减法,最后算括号外面的除.
点评:考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算律简便计算.
=(25×4)×(1.25×8),
=100×10,
=1000;
(2)(3.75+4.1+2.35)×9.8,
=[(3.75+2.35)+4.1]×9.8,
=[6.1+4.1]]×9.8,
=(10+0.2)×(10-0.2),
=100-0.04,
=99.96;
(3)12×(
 +
+ -
- ),
),=12×
 +12×
+12× -12×
-12× ,
,=3+2-4,
=1;
(5)(
 +
+ )÷
)÷ +
+ ,
,=
 ×
× +
+ ,
,=
 +
+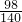 ,
,=
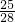 ;
;(6)10÷[
 -(
-( ÷
÷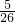 +
+ )],
)],=10÷[
 -(2+
-(2+ )]
)]=10÷[
 -
- ],
],=10÷
 ,
,=
 .
.分析:(1)25×1.25×32把32拆成4×8,利用乘法的结合律变成(25×4)×(1.25×8)计算简便;
(2)(3.75+4.1+2.35)×9.8把括号里的((3.75+4.1+2.35)变成[(3.75+2.35)+4.1]=6.1+4.1=10.2,再把9.8变成(10-0.2)平方差公式变成(10+0.2)×(10-0.2)计算;
(3)12×(
 +
+ -
- )利用乘法的结合律变成12×
)利用乘法的结合律变成12× +12×
+12× -12×
-12× 计算简便;
计算简便;(4)(20.2×0.4+7.88)÷4.2利用四则运算的顺序,先算括号里的20.2×0.4再算括号里的加,最后算除;
(5)(
 +
+ )÷
)÷ +
+ 利用四则运算的顺序,先算括号里的加再算括号外的除,最后算加;
利用四则运算的顺序,先算括号里的加再算括号外的除,最后算加;(6)10÷[
 -(
-( ÷
÷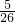 +
+ )]先算括号里的除再算括号里的加,然后算中括号里面的减法,最后算括号外面的除.
)]先算括号里的除再算括号里的加,然后算中括号里面的减法,最后算括号外面的除.点评:考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算律简便计算.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目