题目内容
 如图,点A、O、C在一直线上,OE是∠BOC的平分线,∠EOF=90°,∠1比∠2大75°.
如图,点A、O、C在一直线上,OE是∠BOC的平分线,∠EOF=90°,∠1比∠2大75°.
(1)求∠2的度数.
(2)求∠COF的度数.
解:(1)由题意有:
180°-2∠2-∠2=75°,
180°-3∠2=75°,
3∠2=180°-75°,
3∠2=105°,
∠2=35°.
答:∠2的度数为35°.
(2)∠COF=∠EOF-∠2=90°-35°=55°.
答:∠COF的度数为55°.
分析:(1)根据角平分线的定义可得∠BOC=2∠2,利用平角的定义得到∠1=180°-2∠2,根据等量关系∠1比∠2大75°,得出关于∠2的一元一次方程,解方程即可求得∠2的度数.
(2)根据图形根据互余的定义可知∠COF=∠EOF-∠2,列式计算即可求解.
点评:此题考查了角的平分线的性质,平角的定义以及一元一次方程的解法的综合应用.
180°-2∠2-∠2=75°,
180°-3∠2=75°,
3∠2=180°-75°,
3∠2=105°,
∠2=35°.
答:∠2的度数为35°.
(2)∠COF=∠EOF-∠2=90°-35°=55°.
答:∠COF的度数为55°.
分析:(1)根据角平分线的定义可得∠BOC=2∠2,利用平角的定义得到∠1=180°-2∠2,根据等量关系∠1比∠2大75°,得出关于∠2的一元一次方程,解方程即可求得∠2的度数.
(2)根据图形根据互余的定义可知∠COF=∠EOF-∠2,列式计算即可求解.
点评:此题考查了角的平分线的性质,平角的定义以及一元一次方程的解法的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点A、O、C在一直线上,OE是∠BOC的平分线,∠EOF=90°,∠1=(4x+20)°,∠2=(x-10)°.
如图,点A、O、C在一直线上,OE是∠BOC的平分线,∠EOF=90°,∠1=(4x+20)°,∠2=(x-10)°.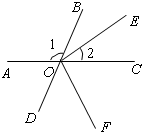 如图,点A、O、C在一直线上,OE是∠BOC的平分线,∠EOF=90°,∠1比∠2大75°.
如图,点A、O、C在一直线上,OE是∠BOC的平分线,∠EOF=90°,∠1比∠2大75°.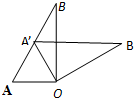 如图,∠AOB=90°,∠B=30°,△A′OB′可以看作是由△AOB绕点O顺时针旋转α角度得到的.若点A′在AB上,则旋转角α的大小可以是( )
如图,∠AOB=90°,∠B=30°,△A′OB′可以看作是由△AOB绕点O顺时针旋转α角度得到的.若点A′在AB上,则旋转角α的大小可以是( )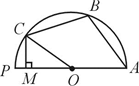 如图,一个半圆的圆心为O,一束光由点M沿垂直于PA的方向射向半圆,光线在圆周上的点C处反射,反射角∠OCB等于入射角∠MCO;接着这束光再与圆周交于点B,依同样方式反射,最后光射入点A,则∠COM=
如图,一个半圆的圆心为O,一束光由点M沿垂直于PA的方向射向半圆,光线在圆周上的点C处反射,反射角∠OCB等于入射角∠MCO;接着这束光再与圆周交于点B,依同样方式反射,最后光射入点A,则∠COM=