题目内容
正方形的一条边增加18厘米，另一条边减少9厘米，结果得到一个与原正方形面积相等的长方形．原正方形的面积是
324
324
平方厘米．分析：要求原正方形的面积，应知道原来的边长．依据条件“得到的长方形与原正方形面积相等”，将数据代入公式即可求得结果．
解答：解：如图所示，
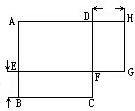
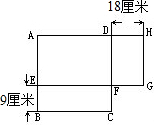
设原正方形的边长为x厘米，如图，由于正方形ABCD与长方形AEGH面积相等，而长方形AEFD是正方形ABCD和长方形AEGH的公共部分，所以长方形EBCF的面积等于长方形DFGH的面积，于是
18×（x-9）-9x=0，
18x-162-9x=0，
18x-9x=162，
9x=162，
x=18；
所以原正方形的面积是：
18×18=324（平方厘米）．
故答案为：324．
设原正方形的边长为x厘米，如图，由于正方形ABCD与长方形AEGH面积相等，而长方形AEFD是正方形ABCD和长方形AEGH的公共部分，所以长方形EBCF的面积等于长方形DFGH的面积，于是
18×（x-9）-9x=0，
18x-162-9x=0，
18x-9x=162，
9x=162，
x=18；
所以原正方形的面积是：
18×18=324（平方厘米）．
故答案为：324．
点评：此题主要考查长方形的面积公式及图形面积的大小关系，将数据代入公式即可求得结果．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
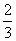等于乙队人数的
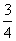，甲队与乙队的人数比是8：9。