题目内容
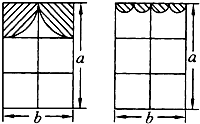 方方和圆圆的房间窗帘的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径都分别相同),它们的窗户能射进阳光的面积分别是多少(窗框面积不计)?谁的窗户射进阳光的面积大?
方方和圆圆的房间窗帘的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径都分别相同),它们的窗户能射进阳光的面积分别是多少(窗框面积不计)?谁的窗户射进阳光的面积大?分析:观察图,可知方方和圆圆的房间窗户的面积相等,都是ab;要求它们的窗户能射进阳光的面积分别是多少,先利用圆的面积S=πr2分别求出两家窗帘的面积,也就是遮住阳光的面积,进而用总面积减去遮住的面积即可.
解答:解:方方家:ab-
×π×(
)2=ab-
π;
圆圆家:ab-2×π×(
)2=ab-
π;
因为ab-
π<ab-
π;
所以圆圆家的窗户能射进阳光的面积大一些.
答:方方家的窗户能射进阳光的面积分别是ab-
π,圆圆家的窗户能射进阳光的面积ab-
π;圆圆家窗户射进阳光的面积大一些.
| 1 |
| 2 |
| b |
| 2 |
| b2 |
| 8 |
圆圆家:ab-2×π×(
| b |
| 8 |
| b2 |
| 32 |
因为ab-
| b2 |
| 8 |
| b2 |
| 32 |
所以圆圆家的窗户能射进阳光的面积大一些.
答:方方家的窗户能射进阳光的面积分别是ab-
| b2 |
| 8 |
| b2 |
| 32 |
点评:解决此题关键是用窗户的面积减去窗帘的面积,就是能射进阳光的面积.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
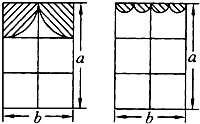 方方和圆圆的房间窗帘的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径都分别相同),它们的窗户能射进阳光的面积分别是多少(窗框面积不计)?谁的窗户射进阳光的面积大?
方方和圆圆的房间窗帘的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径都分别相同),它们的窗户能射进阳光的面积分别是多少(窗框面积不计)?谁的窗户射进阳光的面积大?