题目内容
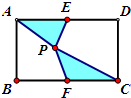如图，ABCD是长为8，宽为6的长方形E、F分别是AD、BC的中点，P为长方形内任一点，求阴影部分的面积？
解：设三角形APE的边AE上的高为h1，三角形CPF的边CF上的高为h2，
×8×h1×+×8×h2×，
=2h1+2h2，
=2×（h1+h2），
=2×6，
=12；
答：阴影部分的面积为12．
分析：由图意可知：三角形APE的边AE上的高，与三角形CPF的边CF上的高的和等于长方形的宽，而AE与CF的都等于长方形的长的一半，利用三角形的面积公式即可求解．
点评：解答此题的关键是：求出两个三角形的底和高与长方形的长和宽的关系．
×8×h1×+×8×h2×，=2h1+2h2，
=2×（h1+h2），
=2×6，
=12；
答：阴影部分的面积为12．
分析：由图意可知：三角形APE的边AE上的高，与三角形CPF的边CF上的高的和等于长方形的宽，而AE与CF的都等于长方形的长的一半，利用三角形的面积公式即可求解．
点评：解答此题的关键是：求出两个三角形的底和高与长方形的长和宽的关系．
练习册系列答案
相关题目
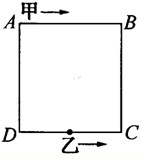如图，ABCD是一个边长为6米的模拟跑道，甲玩具车从A出发顺时针行进，速度是每秒5厘米，乙玩具车从CD的中点出发逆时针行进，结果两车第二次相遇恰好是在B点，求乙车每秒走多少厘米？
如图，ABCD是边长为5的正方形，E、F、G、H分别在边AB、BC、CD、DA上，且AE=BF=CG=DH=3，假定已知AF、BG、CH、DE围成的四边形PQRS是正方形，求图中阴影部分的面积．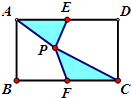
如图，ABCD是长为8，宽为6的长方形E、F分别是AD、BC的中点，P为长方形内任一点，求阴影部分的面积？
如图，ABCD是边长为18厘米的正方形，M、N分别为AB边与BC边上的点，AM：MB=CN：NB=2：1，AN与CM相交于点O，四边形AOCD的面积是