题目内容
下面四个图形a.b.c.d.都是平面图形.
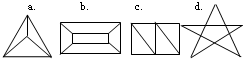
(1)数一数每个图形中各有多少个顶点;多少条边;这些边圈出了多少区域.并将结果填在下表中.
(2)观察表,推断一个平面图形的顶点数,边数,区域数之间的关系式为:
(3)已知某一个平面图形的顶点数为2008,区域数为2007.根据你的推断,这个图形有

(1)数一数每个图形中各有多少个顶点;多少条边;这些边圈出了多少区域.并将结果填在下表中.
| 图形 | 顶点数 | 边数 | 区域数 |
| a | 4 | 6 | 3 |
| b | |||
| c | |||
| d |
顶点数+区域数-边数=1
顶点数+区域数-边数=1
.(3)已知某一个平面图形的顶点数为2008,区域数为2007.根据你的推断,这个图形有
4014
4014
条边.分析:根据图中的四个平面图形数出其顶点数、边数、区域数得题(1)的结果,再根据表(1)数据总结出归律得题(2)的结果,根据题(2)的公式把2008个顶点和2007个区域代入即可得平面图形的边数.
解答:解:(1)观察图形,可以完成填表如下:
(2)根据上表中的顶点数、边数和区域数的数量关系可得:顶点数+区域数-边数=1,
(3)由上可得:平面图形的边数=顶点数+区域数-1;把2008个顶点和2007个区域代入即可得出边数为:
2008+2007-1=4014(条),
故答案为:(2)顶点数+区域数-边数=1;(3)4014.
| 图形 | 顶点数 | 边数 | 区域数 |
| a | 4 | 6 | 3 |
| b | 8 | 12 | 5 |
| c | 6 | 9 | 4 |
| d | 10 | 15 | 6 |
(3)由上可得:平面图形的边数=顶点数+区域数-1;把2008个顶点和2007个区域代入即可得出边数为:
2008+2007-1=4014(条),
故答案为:(2)顶点数+区域数-边数=1;(3)4014.
点评:本题主要考查考生通过观察、分析识图并能总结出相应规律解决问题的能力.

练习册系列答案
相关题目