Question

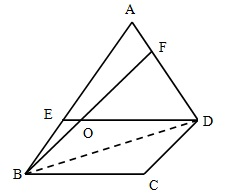（2005?宜兴市）如图所示，在四边形ABCD中，AB=3BE，AD=3AF，平行四边形BODC的面积是69平方厘米．四边形AEOF的面积是

69

2

平方厘米．

Answer 1

分析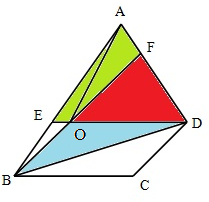：如图，要求四边形AEOF的面积，只要求得S△AOE和S△AOF的面积即可，根据已知平行四边形的面积是69平方厘米，可知△BOD=

69

2

平方厘米；据燕尾定理得出S△AOB：S△DOB=AF：DF=1：2；同理，可以得出S△AOD：S△BOD=AE：BE=2：1；S△AOE：S△BEO=2：1；S△AOF：S△DOF=1：2；换算一下，可以得到S△AOE=

2

3

×S△BOD，S△AOF=

1

3

×S△BOD；所以可得：S△AOE+S△AOF=S△BOD；由此即可求得四边形AEOF的面积．

解答：解：根据燕尾定理得出S△AOB：S△DOB=AF：DF=1：2；
同理，可以得出S△AOD：S△BOD=AE：BE=2：1；S△AOE：S△BEO=2：1；S△AOF：S△DOF=1：2；
换算一下，可以得到S△AOE=

1

3

×S△BOD，S△AOF=

2

3

×S△BOD；
又因为S△BOD=69÷2=

69

2

（平方厘米）；
所以S△AOE+S△AOF=

1

3

×S△BOD+

2

3

×S△BOD=S△BOD=

69

2

（平方厘米）；
答：四边形AEOF的面积是

69

2

平方厘米．
故答案为：

69

2

．

点评：此题考查了利用燕尾定理解决计算图形面积问题的灵活应用，燕尾定理是指两个共一条边的三角形，连接它们不公共的顶点所得到的线段被它们公共边所分的比例就是它们的面积之比．