题目内容
【题目】如图,把从1开始连续的自然数按照一定的顺序排成数表,如果这个数表有40行,请通过计算回答下列问题:
(1)第1行的数是多少?
(2)第20行中的最大数与最小数之和是多少?
(3)第35行中的最大数与最小数之和是多少?
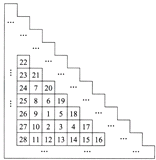
【答案】(1)1,6,7,21,22,45,46,(2)878;(3)1222.
【解析】
试题分析:(1)根据图示,可得第40行有40个数,则一共有数:1+2+3+…+40=(1+40)×40÷2=820(个);第1行的数是:820﹣40+1=781;
(2)分别求出第20行中的最大数与最小数分别是多少,然后相加,求出它们的和是多少;
(3)分别求出第35行中的最大数与最小数分别是多少,然后相加,求出它们的和是多少.
解:根据图示,可得第40行有40个数,
则一共有数:1+2+3+…+40=(1+40)×40÷2=820(个);
(1)第1行的数是:820﹣40+1=781;
当表的层数只有1、4、7、…、40层时,
1的位置在(倒数行数,左数列数):(1,1)、(2,2)、(3,3)、…、(14,14),
一共有数1,10,28,55,91,…;
从1所在的位置往上,每行的最小数:1,6,7,21,22,45,46,
(2)第20行中的最大数是:781+20﹣1=800,
第20行中的最小数是:91﹣13=78,
因此第20行中的最大数与最小数之和是:
800+78=878;
(3)从1所在的位置往下,每行的最小数:2,11,29,56,92,…,
第35行为倒数第6行,最小数为:
2+[1+2+…+(15﹣6)]×9
=2+[1+2+…+9]×9
=2+45×9
=407
第35行中的最大数是:820﹣5=815,
因此第35行中的最大数与最小数之和是:
815+407=1222.

【题目】如图是我国2001﹣﹣2004年废水排放量统计图.

根据统计图完成统计表:
年份 排放量/亿吨 名称 | 2001 | 2002 | 2003 | 2004 |
工业废水 | ||||
生活废水 |
(1)我国工业废水排放量从2001﹣﹣2004年发生了怎样的变化?
(2)我国生活废水排放量从2001﹣﹣2004年发生了怎样的变化?
(3)根据图中的信息,谈谈你的想法.
【题目】某电器城2011年下半年空调和冰箱销售台数如下:
月份 台数 种类 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
空调 | 450 | 750 | 550 | 350 | 250 | 600 |
冰箱 | 300 | 500 | 350 | 300 | 250 | 200 |
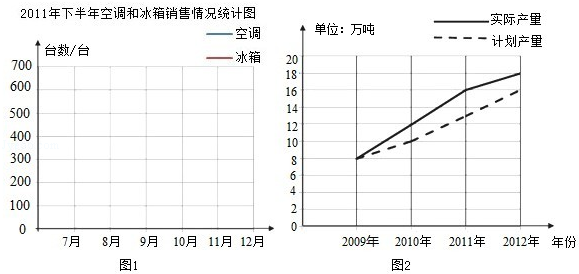
(1)根据上表中的数据制成折线统计图(如图1)。
(2)平均每月销售空调多少台?
(3)如果每台冰箱获利100元,那么这个电器城2011年下半年冰箱销售中共获利多少万元?
(4)下面是某啤酒厂2009~2012年啤酒产量情况统计图如图2.请根据统计图完成下面的统计表、
某啤酒厂2009~2012年啤酒产量情况 统计表
年份 | 2009年 | 2010年 | 2011年 | 2012年 | 合计 |
计划产量 | |||||
实际产量 |