Question

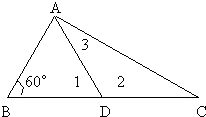如右图，已知AD=BD=CD，∠B=60°，求图∠1、∠2、∠3的度数．

Answer 1

分析：如图：

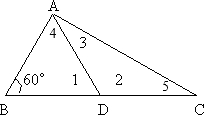
根据AD=BD可知：该三角形为等腰三角形，两底角相等，即∠B=∠4，因为∠B=60°，所以∠4=60°，因为三角形的内角和180°，所以∠1=180°-60°-60°=60°；因为平角是180度，所以∠2=180°-60°=120°，在△ADC中，用“180°-120°=60°”求出∠3和∠5的度数和，又因为AD=DC，所以∠3=∠5，用“60°÷2”解答求出∠3的度数．

解答：解：如图：因为AD=BD，所以∠B=∠4，又因为∠B=60°，所以∠4=60°，在△ABD中，
∠1=180°-60°-60°=60°，
∠2=180°-∠1=180°-60°=120°，
在三角形ADC中，AD=DC，所以：
∠3=（180°-120°）÷2=30°；
答：∠1=60°，∠2=120°，∠3=30°．

点评：解答此题用到的知识点：（1）三角形的内角和是180度；（2）平角的含义；（3）等腰三角形两底角相等的特征．