题目内容
图中阴影部分甲的面积比乙多57平方厘米,直径AB的长为20cm,求CB的长.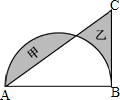
解:由题意可知:
半圆面积=π×( )2÷2,
)2÷2,
=3.14×102÷2,
=3.14×100÷2,
=157(平方厘米);
所以:SABC=157-57=100(平方厘米),
SABC=BC×AB÷2,
100=BC×20÷2,
BC=10(厘米);
答:BC的长为10厘米.
分析:根据图可知空白处是半圆和三角形的公有部分,阴影部分甲的面积比阴乙的面积多57平方厘米,也就是说半圆比三角形ABC的面积大57平方厘米,又因为已知直径,可求出半圆的面积,用半圆面积减去57平方厘米就是三角形的面积,最后根据三角形的面积公式可以求出BC的长.
点评:此题考查了组合图形的面积中,转化思想的灵活应用.
半圆面积=π×(
 )2÷2,
)2÷2,=3.14×102÷2,
=3.14×100÷2,
=157(平方厘米);
所以:SABC=157-57=100(平方厘米),
SABC=BC×AB÷2,
100=BC×20÷2,
BC=10(厘米);
答:BC的长为10厘米.
分析:根据图可知空白处是半圆和三角形的公有部分,阴影部分甲的面积比阴乙的面积多57平方厘米,也就是说半圆比三角形ABC的面积大57平方厘米,又因为已知直径,可求出半圆的面积,用半圆面积减去57平方厘米就是三角形的面积,最后根据三角形的面积公式可以求出BC的长.
点评:此题考查了组合图形的面积中,转化思想的灵活应用.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
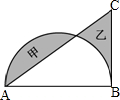

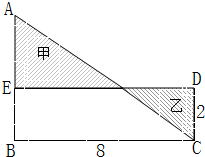 图中,阴影部分甲的面积比乙大4平方厘米.求三角形ABC的面积是
图中,阴影部分甲的面积比乙大4平方厘米.求三角形ABC的面积是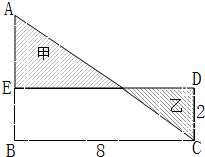 图中,阴影部分甲的面积比乙大4平方厘米.求三角形ABC的面积是________
图中,阴影部分甲的面积比乙大4平方厘米.求三角形ABC的面积是________