题目内容
在一个半径为2厘米的圆内，作出一个最大的正三角形，保留作图根据．
分析：（1）根据圆心确定圆的位置，半径确定圆的大小，由此即可画出一个以O为圆心，以2厘米为半径的圆，
（2）在圆上任意找到一点，以圆的半径为半径画圆，两圆会得到两个交点，再以两点中任意一点为圆心，两点距离为半径作圆，即可求得三角形的第三个顶点，由此顺次连接这三个点即可得到这个圆内最大的正三角形．
（2）在圆上任意找到一点，以圆的半径为半径画圆，两圆会得到两个交点，再以两点中任意一点为圆心，两点距离为半径作圆，即可求得三角形的第三个顶点，由此顺次连接这三个点即可得到这个圆内最大的正三角形．
解答：解：（1）根据题干分析，以O为圆心，以2厘米为半径画圆，如图所示：
（2）在圆上任意找到一点，以圆的半径为半径画圆，两圆会得到两个交点，
再以两点中任意一点为圆心，两点之间的距离为半径作圆，即可求得三角形的第三个顶点，
由此顺次连接这三个点即可得到这个圆内最大的正三角形，如图所示．
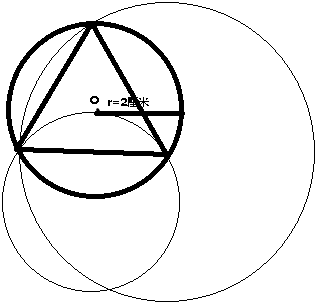
（2）在圆上任意找到一点，以圆的半径为半径画圆，两圆会得到两个交点，
再以两点中任意一点为圆心，两点之间的距离为半径作圆，即可求得三角形的第三个顶点，
由此顺次连接这三个点即可得到这个圆内最大的正三角形，如图所示．
点评：此题考查了圆的画法以及圆内最大的正三角形的画法．
练习册系列答案
金钥匙试卷系列答案
相关题目
（2008?高邮市）在方格纸（每个方格的边长表示1cm）上按以下要求画出图形B、图形C和图形D．