题目内容
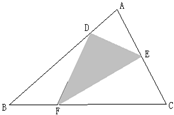 (2013?北京模拟)如图:BD:AB=3:4,AE=EC,BF:FC=1:2,如果三角形ABC的面积是48平方厘米,求阴影部分的面积是
(2013?北京模拟)如图:BD:AB=3:4,AE=EC,BF:FC=1:2,如果三角形ABC的面积是48平方厘米,求阴影部分的面积是14
14
平方厘米.分析:根据三角形各个边的关系,可求出空白处的3个三角形的面积各占三角形ABC面积的几分之几,把三角形ABC看作单位“1”,用单位“1”减去空白部分三角形BFD、三角形CEF、三角形AED各占三角形ABC的份数,就可得到阴影部分占三角形ABC的份数,根据求一个数的几分之几是多少,可用乘法进行计算.
解答:解:根据BD:AB=3:4,BF:FC=1:2,
那么三角形DBF的高为三角形ABC的
,
底为三角形ABC的
,
三角形BDF的面积为大三角形ABC的
×
=
;
同理可得:
三角形EFC的面积为大三角形ABC的
×
=
,
三角形AED的面积为大三角形ABC的
×
=
;
则DEF的面积占三角形ABC的面积的比例为:
[1-(
+
+
)=
,
已知,三角形ABC的面积是48,
则三角形DEFC的面积:48×
=14(平方厘米);
答:阴影部分的面积是14平方厘米.
故答案为:14.
那么三角形DBF的高为三角形ABC的
| 3 |
| 4 |
底为三角形ABC的
| 1 |
| 3 |
三角形BDF的面积为大三角形ABC的
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
同理可得:
三角形EFC的面积为大三角形ABC的
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
三角形AED的面积为大三角形ABC的
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
则DEF的面积占三角形ABC的面积的比例为:
[1-(
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 8 |
| 7 |
| 24 |
已知,三角形ABC的面积是48,
则三角形DEFC的面积:48×
| 7 |
| 24 |
答:阴影部分的面积是14平方厘米.
故答案为:14.
点评:解答此题的关键是分析出空白部分的各条边与三角形ABC各边的关系,再利用求一个数的几分之几是多少的知识点进行解答.

练习册系列答案
相关题目