题目内容
 如图,已知平行四边形ABCD的面积为12cm2,CE=
如图,已知平行四边形ABCD的面积为12cm2,CE= CD,AE与BD的交点为F,求图中阴影部分的面积?
CD,AE与BD的交点为F,求图中阴影部分的面积?
解:因为ABCD是平行四边形,所以CD∥AB,
所以 =
=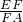 ,
,
又因为CE= ED,所以
ED,所以 =
= ,
,
即,EF:FA=2:3,DE= AB=
AB= CD,
CD,
△AED的面积= ×CD×h÷2,
×CD×h÷2,
= ×12÷2,
×12÷2,
=4(平方厘米),
所以△DFE的面积=4÷(2+3)×2,
= (平方厘米),
(平方厘米),
又因为△BCD的面积= 平行四边形ABCD,
平行四边形ABCD,
所以△BCD=12× =6(平方厘米);
=6(平方厘米);
用△BCD的面积减去△DEF的面积就是阴影部分的面积,
即,6- =
= =4
=4 (平方厘米);
(平方厘米);
图中阴影部分的面积是4 平方厘米.
平方厘米.
分析:我们通过三角形的相似求出EF与FA的比,进一步求出△DEF的面积,再运用大△BCD的面积减去△DEF的面积就是阴影部分的面积.
点评:本题运用了三角形的相似及三角形的面积公式,考查了学生分析,解决问题的方法与能力.
所以
 =
=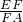 ,
,又因为CE=
 ED,所以
ED,所以 =
= ,
,即,EF:FA=2:3,DE=
 AB=
AB= CD,
CD,△AED的面积=
 ×CD×h÷2,
×CD×h÷2,=
 ×12÷2,
×12÷2,=4(平方厘米),
所以△DFE的面积=4÷(2+3)×2,
=
 (平方厘米),
(平方厘米),又因为△BCD的面积=
 平行四边形ABCD,
平行四边形ABCD,所以△BCD=12×
 =6(平方厘米);
=6(平方厘米);用△BCD的面积减去△DEF的面积就是阴影部分的面积,
即,6-
 =
= =4
=4 (平方厘米);
(平方厘米);图中阴影部分的面积是4
 平方厘米.
平方厘米.分析:我们通过三角形的相似求出EF与FA的比,进一步求出△DEF的面积,再运用大△BCD的面积减去△DEF的面积就是阴影部分的面积.
点评:本题运用了三角形的相似及三角形的面积公式,考查了学生分析,解决问题的方法与能力.

练习册系列答案
相关题目
 如图,已知平行四边形ABCD的面积为12cm2,CE=
如图,已知平行四边形ABCD的面积为12cm2,CE=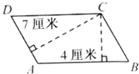 如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.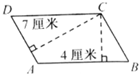 如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
