��Ŀ����
����Ŀ����֪n�ζ���ʽPn(x)=a0xn+a1xn-1+��+an-1x+an,�����һ���㷨��,����![]() (k=2,3,4,��,n)��ֵ��Ҫk-1�γ˷�,
(k=2,3,4,��,n)��ֵ��Ҫk-1�γ˷�,
(1)����P3(x0)��ֵ��Ҫ9������(6�γ˷�,3�μӷ�),�����Pn(x0)��ֵ��Ҫ���ٴ�����?
(2)����ȡ�ؾ����㷨:P0(x)=a0,Pk+1(x)=xPk(x)+ak+1(k=0,1,2,��,n-1),����P3(x0)��ֵֻ��6������,�����Pn(x0)��ֵ����Ҫ���ٴ�����?
(3)����ȡ�ؾ����㷨,��ai=i+1,i=0,1,��,n,��P5(2)(д����ȡ�ؾ����㷨�ļ������).
���𰸡�(1)![]() , (2)2n, (3)120
, (2)2n, (3)120
�������������������1��������ͨ���㷨���㣬����˷���Ҫ![]() �Σ���Ҫ�ӷ�n�Σ��Ӷ��õ��𰸣���2�������ؾ����㷨������ʽ������Ҫ�˷�n�Σ��ӷ�n�Σ���3����P0(x)=a0,
�Σ���Ҫ�ӷ�n�Σ��Ӷ��õ��𰸣���2�������ؾ����㷨������ʽ������Ҫ�˷�n�Σ��ӷ�n�Σ���3����P0(x)=a0,
Pk+1(x)=xPk(x)+ak+1,���㼴��.
���������
ֱ�ӷ��г˷�����Ĵ������ɴﵽ![]() ,�ӷ����n��.�ؾ����㷨ͨ��ת���ѳ˷�����Ĵ������ٵ����n��,�ӷ����n��.
,�ӷ����n��.�ؾ����㷨ͨ��ת���ѳ˷�����Ĵ������ٵ����n��,�ӷ����n��.
(1)![]() .
.
(2)2n.
(3)��ΪP0(x)=a0,
Pk+1(x)=xPk(x)+ak+1,
����P0(2)=1,P1(2)=2P0(2)+2=4,
P2(2)=2P1(2)+3=11,
P3(2)=2P2(2)+4=26,
P4(2)=2P3(2)+5=57,
P5(2)=2P4(2)+6=120.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ�����������꼶һ������������Զ���Եijɼ���¼������λ�����ף�
101 102 95 96 104 82
92 100 89 86 88 109
103 94 99 107 98 106
��1����������ͳ�Ʊ���
�ɼ���cm�� | �ϼ� | 80��89 | 90��99 | 100��109 |
�� �� |
��2���ɼ���90��������Ϊ�����������ﵽ������� ����
��3�����ݱ������ݣ�������������ͳ��ͼ��
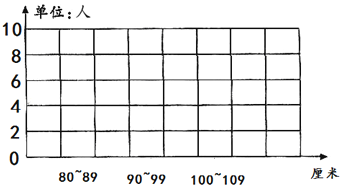
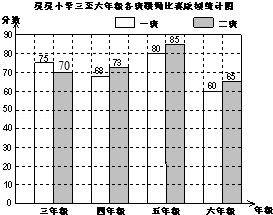
����Ŀ������Сѧ�������꼶�������������ɼ�ͳ��ͼ��
��1���۲�ͳ��ͼ�������������ͳ�Ʊ���
����Сѧ�������꼶��������ͳ�Ʊ�
| ���꼶 | ���꼶 | ���꼶 | ���꼶 |
һ�� | ||||
���� |
��2��ƽ��ÿ��ö��ٷ֣�