题目内容
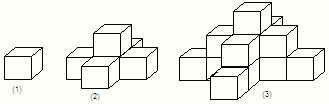
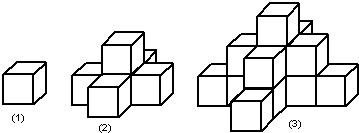
如图是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第11个叠放的图形,小正方体木块总数是________.
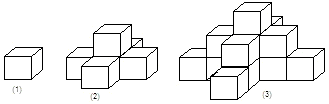
解:分别观察正方体的个数为:1,1+5,1+5+9,…
归纳可知,第n个叠放图形中共有n层,构成了以1为首项,以4为公差的等差数列
所以Sn=n+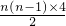 =2n2-n
=2n2-n
当n=11时,2×112-11=231(个),
答:当摆至11层时,正方体的总个数为231个.
故答案为:231.
分析:图(1)中只有一层,有(4×0+1)一个正方形,
图(2)中有两层,在图(1)的基础上增加了一层,第二层有(4×1+1)个.
图(3)中有三层,在图(2)的基础长增加了一层,第三层有(4×2+1),
依次类推总结规律当有n层时总的正方形个数.
点评:本题主要考查归纳推理,其基本思路是先分析具体,观察,总结其内在联系,得到一般性的结论,若求解的项数较少,可一直推理出结果,若项数较多,则要得到一般求解方法,再求具体问题.
归纳可知,第n个叠放图形中共有n层,构成了以1为首项,以4为公差的等差数列
所以Sn=n+
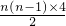 =2n2-n
=2n2-n当n=11时,2×112-11=231(个),
答:当摆至11层时,正方体的总个数为231个.
故答案为:231.
分析:图(1)中只有一层,有(4×0+1)一个正方形,
图(2)中有两层,在图(1)的基础上增加了一层,第二层有(4×1+1)个.
图(3)中有三层,在图(2)的基础长增加了一层,第三层有(4×2+1),
依次类推总结规律当有n层时总的正方形个数.
点评:本题主要考查归纳推理,其基本思路是先分析具体,观察,总结其内在联系,得到一般性的结论,若求解的项数较少,可一直推理出结果,若项数较多,则要得到一般求解方法,再求具体问题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
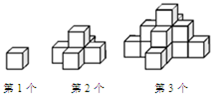 如图,第一个图形是一个水平摆放的小正方体木块,第二个图形和第三个图形是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,若某个叠放的图形中,小正方体木块总数为153个,则这个图形是第
如图,第一个图形是一个水平摆放的小正方体木块,第二个图形和第三个图形是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,若某个叠放的图形中,小正方体木块总数为153个,则这个图形是第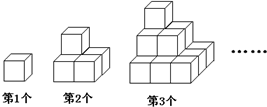 如图,第1个图形是一个水平摆放的小正方体木块,第2个图形和第3个图形是由这样的小正方体叠放而成的.按照这样的规律继续叠放下去,第7个图形中,从正面看,看得到的木块应有
如图,第1个图形是一个水平摆放的小正方体木块,第2个图形和第3个图形是由这样的小正方体叠放而成的.按照这样的规律继续叠放下去,第7个图形中,从正面看,看得到的木块应有