题目内容
【题目】已知:ABCD是长方形,DC=4cm,AD=6cm,E是DF的中点,求S△EFC? 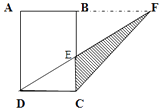
【答案】解:因为AF∥DC,所以三角形DCE∽三角形FBE,CE:BE=DE:FE,由于E是DF的中点,所以E也是DF的中点,
三角形DCE的面积:4×(6÷2)÷2
=4×3÷2
=6(cm2)
三角形DCF的面积:4×6÷2=12(cm2)
三角形EFC的面积:12﹣6=6(cm2)
答:三角形EFC的面积6cm2
【解析】阴影三有形面积等于三角形DCF的面积减去三角形DCE的面积.三角形DCF的底与长方形的宽相等,高与长方形的长相等,长方形的长、宽已知,三角形FDC的面积可求;因为AF∥DC,所以三角形DCE∽三角形FBE,CE:BE=DE:FE,由于E是DF的中点,所以E也是DF的中点,三角形DCE的底等于长方形的宽,高为长方形长的一半,面积可求.

练习册系列答案
相关题目