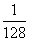题目内容
(1)计算下面各题,然后找出规律.
1-
=
1-
-
=
1-
-
-
=
1-
-
-
-
=
(2)应用上面的规律,直接计算出下面式题的得数.
(1)1-
-
-
-
-
-
-
=
;
(2)
+
+
+
+
+
=
.
1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 16 |
(2)应用上面的规律,直接计算出下面式题的得数.
(1)1-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 128 |
| 1 |
| 128 |
(2)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 63 |
| 64 |
| 63 |
| 64 |
分析:(1)先算出给出的式子的得数,再观察式子与得数,不难发现当1减去连续的偶数的倒数时,差是最后的那个分数;
(2)①根据(1)的规律可以直接写出得数为
;
②设
+
+
+
+
+
=a,则1-a=1-(
+
+
+
+
+
)=1-
-
-
-
-
-
=
,由此求出a的值,即要求的式子的值.
(2)①根据(1)的规律可以直接写出得数为
| 1 |
| 128 |
②设
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 64 |
解答:解:(1)1-
=
,
1-
-
=
,
1-
-
-
=
,
1-
-
-
-
=
,
(2)①1-
-
-
-
-
-
-
=
,
②设
+
+
+
+
+
=a,
则1-a=1-(
+
+
+
+
+
)=1-
-
-
-
-
-
=
,
所以a=1-
=
,
故答案为:
,
,
,
,
,
.
| 1 |
| 2 |
| 1 |
| 2 |
1-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
1-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
1-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
(2)①1-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 128 |
②设
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
则1-a=1-(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 64 |
所以a=1-
| 1 |
| 64 |
| 63 |
| 64 |
故答案为:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 128 |
| 63 |
| 64 |
点评:关键是根据给出的算式与得数得出规律:当1减去连续的偶数的倒数时,差是最后的那个分数,由此解决问题.

练习册系列答案
相关题目
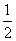 =
= 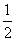 -
-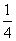 =
= 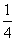 -
-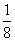 =
= -
-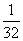 -
-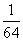 -
-